题目内容
在平面直角坐标系xOy中,直线m的参数方程为
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin2θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
|
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由直线m的参数方程
消去t参数可得:直线m的普通方程.由曲线C的极坐标方程为ρsin2θ=8cosθ化为ρ2sin2θ=8ρcosθ,得到曲线C的普通方程为y2=8x.由题设直线m与曲线C交于A、B两点,设A(x1,y1),B(x2,y2).联立方程化为y2-8y-48=0,利用|AB|=
即可得出.
|
| (1+12)[(y1+y2)2-4y1y2] |
解答:
解:由直线m的参数方程
消去t参数可得:直线m的普通方程为x-y=6.
由曲线C的极坐标方程为ρsin2θ=8cosθ化为ρ2sin2θ=8ρcosθ,得到曲线C的普通方程为y2=8x.
由题设直线m与曲线C交于A、B两点,设A(x1,y1),B(x2,y2).
联立方程
,化为y2-8y-48=0,
则y1+y2=8,y1•y2=-48.
于是|AB|=
=
=16
.
故|AB|=16
.
|
由曲线C的极坐标方程为ρsin2θ=8cosθ化为ρ2sin2θ=8ρcosθ,得到曲线C的普通方程为y2=8x.
由题设直线m与曲线C交于A、B两点,设A(x1,y1),B(x2,y2).
联立方程
|
则y1+y2=8,y1•y2=-48.
于是|AB|=
| (1+12)[(y1+y2)2-4y1y2] |
| 2(82+4×48) |
| 2 |
故|AB|=16
| 2 |
点评:本题考查了参数方程极坐标化为普通方程、直线与抛物线相交弦长问题,考查了计算能力,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
在直角三角形ABC中,∠C=90°,AC=3,取点D,E使
=2
,
=3
,那么
•
+
•
=( )
| BD |
| DA |
| AB |
| BE |
| CD |
| CA |
| CE |
| CA |
| A、3 | B、6 | C、-3 | D、-6 |
已知双曲线一焦点坐标为(0,-5),一渐近线方程为3x+4y=0,则双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
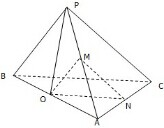 已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.
已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.