题目内容
已知函数f(x)=x2+ex-
(x<0)与g(x)=x2+ln(x+a)图象上存在关y轴对称的点,则a的取值范围是 .
| 1 |
| 2 |
考点:函数的图象
专题:函数的性质及应用
分析:把函数图象点的对称问题转化为a=ee-x-
-x有解即可,利用导数判出最大值,即可得出a的范围.
| 1 |
| 2 |
解答:
解:设x>0,g(x)=x2+ln(x+a)图象上一点P(x,y),
则P′(-x,y)在函数f(x)=x2+ex-
(x<0)的图象上,
∴(-x)2+e-x-
=x2+ln(x+a),
化简得a=ee-x-
-x有解即可,
令h(x)=ee-x-
-x,
则h′(x)=)=ee-x-
•(-e-x)-1=-e-x-
+e-x-1<0,
∴函数h(x)在(0,+∞)上单调递减,
即h(x)<h(0)=
要使a=ee-x-
-x有解,
只需要a<
,即可
故a的取值范围是(-∞,
),
故答案为:(-∞,
)
则P′(-x,y)在函数f(x)=x2+ex-
| 1 |
| 2 |
∴(-x)2+e-x-
| 1 |
| 2 |
化简得a=ee-x-
| 1 |
| 2 |
令h(x)=ee-x-
| 1 |
| 2 |
则h′(x)=)=ee-x-
| 1 |
| 2 |
| 1 |
| 2 |
∴函数h(x)在(0,+∞)上单调递减,
即h(x)<h(0)=
| e |
要使a=ee-x-
| 1 |
| 2 |
只需要a<
| e |
故a的取值范围是(-∞,
| e |
故答案为:(-∞,
| e |
点评:本题考察函数的性质在求解方程有解中的应用,知识综合大,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知{an}是等比数列,对任意n∈N*都有an>0,如果a3(a3+a5)+a4(a4+a6)=25,则a3+a5=( )
| A、5 | B、10 | C、15 | D、20 |
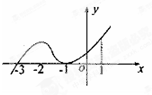 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-3是函数y=f(x)的极小值点;
②-1是函数y=f(x)的极值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
| A、①② | B、①④ | C、②③ | D、③④ |
函数f(x)=
+
的定义域为( )
| 2x+1 |
| 1 |
| x-3 |
| A、(-∞,3)∪(3,+∞) | ||
B、[-
| ||
C、(-
| ||
D、[-
|