题目内容
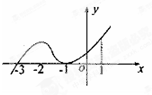 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-3是函数y=f(x)的极小值点;
②-1是函数y=f(x)的极值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
| A、①② | B、①④ | C、②③ | D、③④ |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,导数的综合应用
分析:由图象得出函数的单调区间,函数的极值点.
-3为极小值点,即可判断①;x=-1处的导数左正右正,不为极值点,即可判断②;
y=f(x)在x=0处导数大于0,即切线的斜率大于零,即可判断③;
y=f(x)在区间(-3,1)上单调递增,即可判断④.
-3为极小值点,即可判断①;x=-1处的导数左正右正,不为极值点,即可判断②;
y=f(x)在x=0处导数大于0,即切线的斜率大于零,即可判断③;
y=f(x)在区间(-3,1)上单调递增,即可判断④.
解答:
解:由图象得:
在(-∞,-3)上,f′(x)<0,f(x)递减,
在(-3,+∞)上,f′(x)>0,f(x)递增,
对于①,-3为极小值点,故①正确,
对于②,x=-1处的导数左正右正,不为极值点,故②错误;
对于③,y=f(x)在x=0处切线的斜率大于零,故③错误;
对于④,y=f(x)在区间(-3,1)上单调递增,故④正确.
故选B.
在(-∞,-3)上,f′(x)<0,f(x)递减,

在(-3,+∞)上,f′(x)>0,f(x)递增,
对于①,-3为极小值点,故①正确,
对于②,x=-1处的导数左正右正,不为极值点,故②错误;
对于③,y=f(x)在x=0处切线的斜率大于零,故③错误;
对于④,y=f(x)在区间(-3,1)上单调递增,故④正确.
故选B.
点评:本题考查了函数的单调性,导数的应用,渗透了数形结合思想,是一道中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
若集合A={x|x2-7x<0,x∈N*},B={y|
∈N*}中元素的个数为( )
| 4 |
| y |
| A、3个 | B、2个 | C、1个 | D、0个 |