题目内容
5.设函数y=f(x)的定义域为D,且对任意a∈D,都有唯一的实数b满足f(b)=2f(a)-b,则该函数可能是( )| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=|x| | C. | f(x)=2x | D. | f(x)=x+$\frac{1}{x}$ |
分析 根据已知中对任意a∈D,都有唯一的实数b满足f(b)=2f(a)-b,逐一分析四个函数是否满足条件,可得结论.
解答 解:∵任意a∈D,都有唯一的实数b满足f(b)=2f(a)-b,
若f(x)=$\frac{1}{x}$,令a=2,则2f(a)=1,
若f(b)=2f(a)-b,则f(b)+b=1,此时不存在满足条件的b值,
故A错误;
若f(x)=|x|,令a=0,则2f(a)=0,
若f(b)=2f(a)-b,则f(b)+b=0,此时,任意b≤0均满足条件,
故B错误;
若f(x)=2x,则满足对任意a∈D,都有唯一的实数b满足f(b)=2f(a)-b,
故C正确;
若f(x)=x+$\frac{1}{x}$,令a=1,则2f(a)=4,
若f(b)=2f(a)-b,则f(b)+b=4,则存在两个b值满足条件,
故D错误,
故选:C
点评 本题考查的知识点是新定义,函数图象和性质,函数的零点与方程根的关系,难度中档.

练习册系列答案
相关题目
15.已知集合A={x|log2x<2},B={y|y=3x+2,x∈R},则A∩B=( )
| A. | (1,4) | B. | (2,4) | C. | (1,2) | D. | (1,+∞) |
13.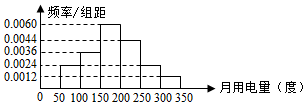 为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
 为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )
为了了解长沙市居民月用电情况,抽查了该市100户居民用电量(单位:度),得到频率分布直方图如下:根据如图可得到这100户居民月用电量在[150,300]的用户数是( )| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
4.已知i为虚数单位,若复数i•z=$\sqrt{2}$-i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.在复平面内,复数g(x)满足$z({1+i})=|{1+\sqrt{3}i}|$,则z的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |