题目内容
20.已知等差数列{an}的首项a1=1,公差d>0,且a52=a2a14.(1)求数列{an}的前n项和Sn;
(2)若数列{bn}的满足b1+2b2+3b3+…+nbn-n=$\frac{{S}_{n}}{2}$,求数列{bn}的通项公式.
分析 (1)利用等差数列与等比数列的通项公式及其前n项和公式即可得出.
(2)利用递推关系即可得出.
解答 解:(1)∵a52=a2a14,
∴(1+4d)2=(1+d)(1+13d),解得d=2.
∴an=1+(n-1)×2=2n-1.
Sn=$\frac{n(1+2n-1)}{2}$=n2.
(2)∵数列{bn}的满足b1+2b2+3b3+…+nbn-n=$\frac{{S}_{n}}{2}$,
∴b1-1=$\frac{{a}_{1}}{2}$,解得b1=$\frac{3}{2}$.
当n≥2时,b1+2b2+3b3+…+(n-1)bn-1-(n-1)=$\frac{{S}_{n-1}}{2}$,
可得:nbn-1=$\frac{{a}_{n}}{2}$=$\frac{2n-1}{2}$,
可得bn=$\frac{2n+1}{2n}$.当n=1时也成立.
∴bn=$\frac{2n+1}{2n}$.
点评 本题考查了递推关系、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
10.复数$\frac{2-i}{1+{i}^{5}}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知两集合A={x|x2+x-2≤0},B={x|$\frac{1}{x}<2$},则A∩B=( )
| A. | [-2,0) | B. | ($\frac{1}{2}$,1] | C. | [-2,0)∪($\frac{1}{2}$,1] | D. | [1,+∞) |
5.设函数y=f(x)的定义域为D,且对任意a∈D,都有唯一的实数b满足f(b)=2f(a)-b,则该函数可能是( )
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=|x| | C. | f(x)=2x | D. | f(x)=x+$\frac{1}{x}$ |
9.已知A为△ABC的最小内角,若向量$\overrightarrow{a}$=(cos2A,sin2A),$\overrightarrow{b}$=($\frac{1}{co{s}^{2}A+1}$,$\frac{1}{si{n}^{2}A-2}$),则$\overrightarrow{a}$$•\overrightarrow{b}$的取值范围是( )
| A. | (-∞,$\frac{1}{2}$) | B. | (-1,$\frac{1}{2}$) | C. | [-$\frac{2}{5}$,$\frac{1}{2}$) | D. | [-$\frac{2}{5}$,+∞) |
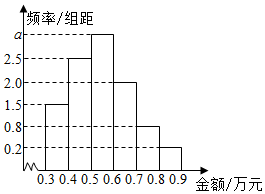 某电子商务公司对10000名网络购物者2015年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9],其频率分布直方图如图所示,在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为( )
某电子商务公司对10000名网络购物者2015年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9],其频率分布直方图如图所示,在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为( )