题目内容
18．已知集合A={2，4，6，8}，$B=\left\{{x|y=\sqrt{4-x}}\right\}$，则A∩B=（ ）| A． | {2} | B． | {2，4} | C． | {2，4，6} | D． | ∅ |
分析 根据题意，分析可得集合B函数y=$\sqrt{4-x}$的定义域，则可得集合B，结合集合A，由集合交集的定义计算可得答案．
解答 解：根据题意，$B=\left\{{x|y=\sqrt{4-x}}\right\}$，为函数y=$\sqrt{4-x}$的定义域，
则B={x|x≤4}，
又由集合A={2，4，6，8}，
则A∩B={2，4}；
故选：B．
点评 本题考查集合交集的计算，关键是求出集合B．
练习册系列答案
相关题目
9．
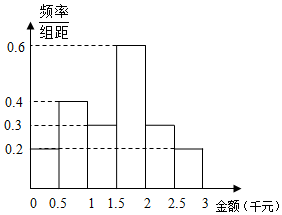某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：
若网购金额超过2千元的顾客称为“网购达人”，网购金额不超过2千元的顾客称为“非网购达人”．
（ I）根据频率分布直方图估计网友购物金额的平均值；
（ II）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
（ I）根据频率分布直方图估计网友购物金额的平均值；
（ II）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
6．执行如图所示的程序框图，若输入t的值为5，则输出的S的值为（ ）
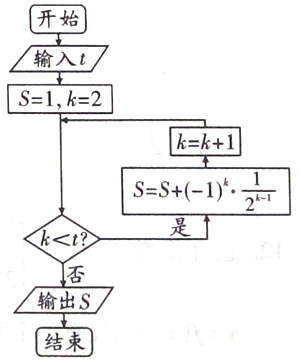
| A． | $\frac{11}{8}$ | B． | $\frac{9}{16}$ | C． | $\frac{5}{4}$ | D． | $\frac{21}{16}$ |
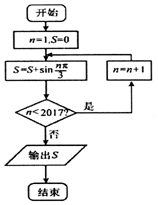
3．执行如图所示的程序框图，则输出 S的值为（ ）
| A． | -lg9 | B． | -1 | C． | -lg11 | D． | 1 |
10．在△ABC中，点M为边BC上任意一点，点N为AM的中点，若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$（λ，μ∈R），则λ+μ的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）的左焦点F与抛物线y2=-4x的焦点重合，直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心，以椭圆的离心率e为半径的圆相切．