题目内容
在正方体ABCD-A1B1C1D1中,下列几种说法正确的是( )
| A、A1C1与B1C成60°角 |
| B、D1C1⊥AB |
| C、AC1与DC成45°角 |
| D、A1C1⊥AD |
考点:空间中直线与直线之间的位置关系,异面直线及其所成的角
专题:空间位置关系与距离
分析:由正方体的性质和异面直线所成的角逐个选项验证可得.
解答:
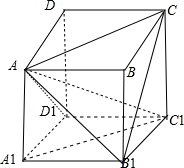
解:如图,∵AC∥A1C1,∴∠ACB1即为A1C1与B1C所成的角,
在正△AB1C中易得,∠ACB1=60°,故A正确;
选项B,由正方体的性质易得D1C1∥AB,故错误;
选项C,可得DC∥D1C1,在RT△AC1D1中,AD1≠D1C1,
故AC1与DC不可能成45°角,故错误;
选项D,易得∠D1A1C1为A1C1与AD所成的角,
在等腰直角三角形D1A1C1为中易得∠D1A1C1=45°,
故A1C1与AD不可能垂直,故错误.
故选:A
在正△AB1C中易得,∠ACB1=60°,故A正确;
选项B,由正方体的性质易得D1C1∥AB,故错误;
选项C,可得DC∥D1C1,在RT△AC1D1中,AD1≠D1C1,
故AC1与DC不可能成45°角,故错误;
选项D,易得∠D1A1C1为A1C1与AD所成的角,
在等腰直角三角形D1A1C1为中易得∠D1A1C1=45°,
故A1C1与AD不可能垂直,故错误.
故选:A

点评:本题考查空间直线与直线的位置关系,涉及异面直线所成的角,属基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
已知全集U={0,1,2,3,4}且∁UA={0,2},则集合A的非空真子集共有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
设A、B为椭圆
+
=1上任意两点,O为坐标原点,则“OA⊥OB”是“O到直线AB的距离为
”的( )
| x2 |
| 16 |
| y2 |
| 9 |
| 12 |
| 5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
已知a,b∈R,且a2>b2( )
| A、若b<0,则a>b |
| B、若b>0,则a<b |
| C、若a>b,则a>0 |
| D、若b>a,则b>0 |
 如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰三角形,∠ACB=90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合),使得点A1到平面AED的距离为
如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰三角形,∠ACB=90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合),使得点A1到平面AED的距离为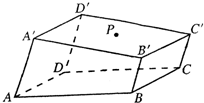 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.