题目内容
已知在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥平面ABCD,AE⊥SB于E,EF⊥SC于F,求证:AF⊥SC.
考点:直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:证明SC⊥平面AEF即可,得到AF⊥SC.
解答:

证明:∵SA⊥平面AC,
∴SA⊥BC.
∵AB⊥BC,且SA∩AB=A,
∴BC⊥平面SAB,
∴BC⊥AE,
又∵AE⊥SB,且SB∩BC=B,
∴AE⊥平面SBC,
∴AE⊥SC,且EF⊥SC,AE∩EF=E,
∴SC⊥平面AEF,
∴AF⊥SC.

证明:∵SA⊥平面AC,
∴SA⊥BC.
∵AB⊥BC,且SA∩AB=A,
∴BC⊥平面SAB,
∴BC⊥AE,
又∵AE⊥SB,且SB∩BC=B,
∴AE⊥平面SBC,
∴AE⊥SC,且EF⊥SC,AE∩EF=E,
∴SC⊥平面AEF,
∴AF⊥SC.
点评:本题重点考查了空间中直线与直线垂直、直线与平面垂直、平面与平面垂直的判定和性质等知识,属于基本知识的考查,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
3<m<5是方程
+
=1表示的图形为双曲线的( )
| x2 |
| m-3 |
| y2 |
| m-8 |
| A、充分但非必要条件 |
| B、必要但非充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
在正方体ABCD-A1B1C1D1中,下列几种说法正确的是( )
| A、A1C1与B1C成60°角 |
| B、D1C1⊥AB |
| C、AC1与DC成45°角 |
| D、A1C1⊥AD |
在直线y=2x+1上有一点P,过点P且垂直于直线4x+3y-3=0的直线与圆x2+y2-2x=0有公共点,则点P的横坐标的取值范围是( )
| A、(-∞,-1)∪(1,+∞) | ||||
| B、(-1,1) | ||||
C、[-
| ||||
D、(-
|
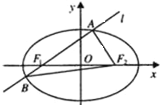 如图,椭圆
如图,椭圆