题目内容
已知全集U={0，1，2，3，4}且∁UA={0，2}，则集合A的非空真子集共有（ ）
| A、5个 | B、6个 | C、7个 | D、8个 |
考点：补集及其运算
专题：计算题,集合
分析：对于有限集合，我们有以下结论：若一个集合中有n个元素，则它有2n个子集．
解答：
解：依题意，A={1，3，4}，
∴集合A的非空真子集共有8-2=6个，
故选B．
∴集合A的非空真子集共有8-2=6个，
故选B．
点评：本题考查了集合的子集个数，若一个集合中有n个元素，则它有2n个子集，有（2n-1）个真子集，属于基础题．
练习册系列答案
相关题目
已知a=log36，b=log510，c=log714，则（ ）
| A、a＜b＜c |
| B、c＜a＜b |
| C、b＜a＜c |
| D、c＜b＜a |
设A={x|x2-4x-5=0}，B={1，2，3，4，5}，则A∩B=（ ）
| A、{1} | B、{5} |
| C、{1，5} | D、∅ |
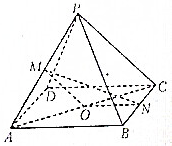如图，在四棱锥P-ABCD中，M、N分别是侧棱PA和底面BC边的中点，O是底面?ABCD对角线AC的中点，求证：过O、M、N三点的平面与侧面PCD平行．在正方体ABCD-A1B1C1D1中，下列几种说法正确的是（ ）
| A、A1C1与B1C成60°角 |
| B、D1C1⊥AB |
| C、AC1与DC成45°角 |
| D、A1C1⊥AD |