题目内容
在四面体O-ABC中,点M在OA上,且OM=2MA,N为BC的中点,若
=
+
+
,则使G与M,N共线的x的值为( )
| OG |
| 1 |
| 3 |
| OA |
| x |
| 4 |
| OB |
| x |
| 4 |
| OC |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点:共线向量与共面向量
专题:空间向量及应用
分析:由已知可得
=
(
+
),
=
.假设G与M,N共线,则存在实数λ使得
=λ
+(1-λ)
=
(
+
)+
,与
=
+
+
比较可得.
| ON |
| 1 |
| 2 |
| OB |
| OC |
| OM |
| 2 |
| 3 |
| OA |
| OG |
| ON |
| OM |
| λ |
| 2 |
| OB |
| OC |
| 2(1-λ) |
| 3 |
| OA |
| OG |
| 1 |
| 3 |
| OA |
| x |
| 4 |
| OB |
| x |
| 4 |
| OC |
解答:
解:
=
(
+
),
=
.
假设G与M,N共线,则存在实数λ使得
=λ
+(1-λ)
=
(
+
)+
,
与
=
+
+
比较可得:
=
,
=
,
解得x=1.
故选:A.
| ON |
| 1 |
| 2 |
| OB |
| OC |
| OM |
| 2 |
| 3 |
| OA |
假设G与M,N共线,则存在实数λ使得
| OG |
| ON |
| OM |
| λ |
| 2 |
| OB |
| OC |
| 2(1-λ) |
| 3 |
| OA |
与
| OG |
| 1 |
| 3 |
| OA |
| x |
| 4 |
| OB |
| x |
| 4 |
| OC |
| 2(1-λ) |
| 3 |
| 1 |
| 3 |
| λ |
| 2 |
| x |
| 4 |
解得x=1.
故选:A.
点评:本题考查了向量的共线定理、向量的平行四边形法则,属于基础题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则它的体积为( )
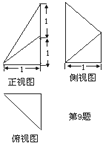

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
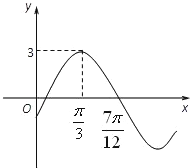 已知函数f(x)=Asin(ωx+ϕ),(其中x∈R,A>0,ω>0,|ϕ|<
已知函数f(x)=Asin(ωx+ϕ),(其中x∈R,A>0,ω>0,|ϕ|<