题目内容

函数y=log2（2x-x2）的单调递增区间是
 
，单调递减区间是
 
．
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=2x-x2＞0，求得函数y的定义域为（0，2），根据y=log2t，函数y的增区间即t在（0，2）上的增区间，y的减区间即t在（0，2）上的减区间，再利用二次函数的性质可得结论．
解答： 解：令t=2x-x2＞0，求得0＜x＜2，故函数y的定义域为（0，2），y=log2t，
故函数y的增区间即t在（0，2）上的增区间，y的减区间即t在（0，2）上的减区间．
利用二次函数的性质可得t在（0，2）上的增区间为（0，1]，t在（0，2）上的减区间为（1，2），
故答案为：（0，1]；（1，2）．
点评：本题主要考查复合函数的单调性，对数函数、二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
已知α、β都是锐角，sinα=
1
7
，cos（α+β）=-
4
5
，求cosβ的值．
已知点P为抛物线y2=4x上的动点，点P在y轴上的射影是M，点A的坐标是（6，5），则|PA|+|PM|的最小值是（　　）
A、8
B、7
C、5
2
D、5
2
-1
已知函数f（x）=x2+（a-1）x+a为偶函数．
（1）求a的值；
（2）设函数，g（x）=
f(x)
x
，当x∈[1，+∞]时，不等式g（x）+f（m）+2m≥5恒成立，求m的取值范围．
计算：
1-sin24°
=
 
．
已知双曲线C：
x2
a2
-
y2
b2
=1的焦点为F（-c，0），F′（c，0），c＞0，过F且平行于双曲线渐近线的直线与抛物线y2=4cx交于点P，若P在以FF′为直径的圆上，则该双曲线的离心率平方为（　　）
A、
3+
5
2
B、
5
C、
5
-1
2
D、
1+
5
2
f（x）是定义在（0，+∞）的函数，且f（xy）=f（x）+f（y）；当x＞1是有f（x）＜0；f（3）=-1
（1）求f（1）和f（
1
9
）的值；
（2）证明f（x）在x＞0上是减函数；
（3）解不等式f（x）+f（2-x）＜2．
已知M（-3，5），N（2，5）在x-y+1=0上找一点P，使|PM|+|PN|最小．
一个几何体的三视图如图所示，则它的体积为（　　）
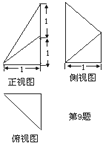
A、
3
2
B、
1
2
C、
3
2
D、
3
2
+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网