题目内容
对于函数f(x)=ex-kx-1(k∈R)的零点,下列判断中正确的个数为( )
①对于?k∈R,函数f(x)总有零点;
②对于?k>1,函数f(x)总有两个零点;
③?k∈(0,1),使得函数f(x)有且仅有一个零点;
④k∈(-∞,0)是函数f(x)有且仅有一个零点的充分不必要条件.
①对于?k∈R,函数f(x)总有零点;
②对于?k>1,函数f(x)总有两个零点;
③?k∈(0,1),使得函数f(x)有且仅有一个零点;
④k∈(-∞,0)是函数f(x)有且仅有一个零点的充分不必要条件.
| A、1 | B、2 | C、3 | D、4 |
考点:函数零点的判定定理
专题:计算题,作图题,函数的性质及应用
分析:令f(x)=ex-kx-1=0,当x=0时,k∈R;当x≠0时,k=
;作函数图象分析.从而对四个命题依次判断.
| ex-1 |
| x |
解答:
解:令f(x)=ex-kx-1=0,
当x=0时,k∈R;
当x≠0时,k=
;
作函数y=
的图象如下,

故①对于?k∈R,函数f(x)总有零点0,故正确;
②对于?k>1,函数f(x)总有两个零点也正确;
③?k∈(0,1),使得函数f(x)总有两个零点,故不正确;
④k∈(-∞,0)是函数f(x)有且仅有一个零点的充分不必要条件,当k=1时也只有一个零点,故正确.
故选C.
当x=0时,k∈R;
当x≠0时,k=
| ex-1 |
| x |
作函数y=
| ex-1 |
| x |

故①对于?k∈R,函数f(x)总有零点0,故正确;
②对于?k>1,函数f(x)总有两个零点也正确;
③?k∈(0,1),使得函数f(x)总有两个零点,故不正确;
④k∈(-∞,0)是函数f(x)有且仅有一个零点的充分不必要条件,当k=1时也只有一个零点,故正确.
故选C.
点评:本题考查了函数的零点的判断与应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如图所示,则它的体积为( )
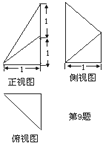

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
任取两个不同的1位正整数,它们的和是8的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|