题目内容
2.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.若直线AF的斜率为$-\sqrt{3}$,则|PF|=( )| A. | $4\sqrt{3}$ | B. | 6 | C. | 8 | D. | 16 |
分析 先根据抛物线方程求出焦点坐标和准线方程,根据直线AF的斜率得到AF方程,与准线方程联立,解出A点坐标,因为PA垂直准线l,所以P点与A点纵坐标相同,再代入抛物线方程求P点横坐标,利用抛物线的定义就可求出|PF|长.
解答 解:∵抛物线方程为y2=8x,
∴焦点F(2,0),准线l方程为x=-2,
∵直线AF的斜率为$-\sqrt{3}$,直线AF的方程为y=$-\sqrt{3}$(x-2),
由$\left\{\begin{array}{l}{x=-2}\\{y=-\sqrt{3}(x-2)}\end{array}\right.$,可得A点坐标为(-2,4$\sqrt{3}$),
∵PA⊥l,A为垂足,
∴P点纵坐标为4$\sqrt{3}$,代入抛物线方程,得P点坐标为(6,4$\sqrt{3}$),
∴|PF|=|PA|=6-(-2)=8,
故选C.
点评 本题主要考查抛物线的几何性质,定义的应用,以及曲线交点的求法,属于综合题.

练习册系列答案
相关题目
13.函数y=sin2(x-$\frac{π}{4}$)的图象沿x轴向右平移m个单位(m>0),所得图象关于y轴对称,则m的最小值为( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
10.设等差数列{an}的公差为d,d≠0,若{an}的前10项之和大于其前21项之和,则( )
| A. | d<0 | B. | d>0 | C. | a16<0 | D. | a16>0 |
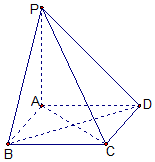 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.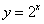 B.
B.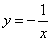
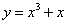 D.
D.