题目内容
7.已知函数$f(x)=sinωx(cosωx-\sqrt{3}sinωx)+\frac{{\sqrt{3}}}{2}(ω>0)$的最小正周期为$\frac{π}{2}$.(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调递减区间.
分析 (1)利用二倍角公式及辅助角公式求得f(x)的解析式,由函数的周期公式即可求得ω的值;
(2)由(1)可知,利用正弦函数的性质,求得函数f(x)的单调递减区间.
解答 解:由$f(x)=sinωx(cosωx-\sqrt{3}sinωx)+\frac{{\sqrt{3}}}{2}$,
=$sinωx•cosωx-\sqrt{3}{sin^2}ωx+\frac{{\sqrt{3}}}{2}$,
=$\frac{1}{2}sin2ωx+\frac{{\sqrt{3}}}{2}cos2ωx$,
=$sin(2ωx+\frac{π}{3})$,…(5分)
(Ⅰ) 又因为函数f(x)的最小正周期为T=$\frac{π}{2}$,
∴$\frac{2π}{2ω}=\frac{π}{2}$.
解得:ω=2.…(7分)
(Ⅱ) 令$2kπ+\frac{π}{2}≤4x+\frac{π}{3}≤2kπ+\frac{3π}{2},k∈Z$,解得:$2kπ+\frac{π}{6}≤4x≤2kπ+\frac{7π}{6},k∈Z$,
∴$\frac{kπ}{2}+\frac{π}{24}≤x≤\frac{kπ}{2}+\frac{7π}{24},k∈Z$.
∴函数f(x)的单调递减区间是$[\frac{kπ}{2}+\frac{π}{24},\frac{kπ}{2}+\frac{7π}{24}],k∈Z$.…(13分)
点评 本题考查辅助角公式及二倍角公式的应用,考查正弦函数图象与性质,考查计算能力,属于中档题.

练习册系列答案
相关题目
2.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.若直线AF的斜率为$-\sqrt{3}$,则|PF|=( )
| A. | $4\sqrt{3}$ | B. | 6 | C. | 8 | D. | 16 |
19.在△ABC中,内角A,B,C所对的边分别为a,b,c,若a=$\sqrt{3}$,A=60°,B=45°,则b的长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |

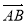 =a,
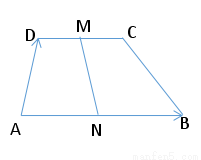
=a,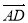 =b,试用a、b分别表示
=b,试用a、b分别表示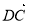 、
、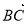 、
、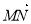 .
.
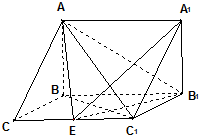 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=$\frac{π}{3}$