题目内容
14．
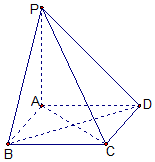如图，棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，BD=$2\sqrt{2}$．求二面角P-CD-B余弦值的大小．
分析 由线面垂直的性质可得PA⊥CD，再由已知得到CD⊥AD，由线面垂直的判定可得CD⊥平面PAD，进一步得到PD⊥CD．得到∠PDA为二面角P-CD-B的平面角，再由已知得答案．
解答 解：∵PA⊥平面ABCD，∴PA⊥CD，
∵底面ABCD是矩形，∴CD⊥AD，
∵又PA∩AD=A，∴CD⊥平面PAD，
则PD⊥CD．
∴∠PDA为二面角P-CD-B的平面角，
在Rt△PAD中，由PA=AD=2，可得∠PDA=45°．
∴二面角P-CD-B余弦值为$\frac{\sqrt{2}}{2}$．
点评 本题考查二面角的平面角的求法，考查线面垂直的判定，是基础题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
2．设抛物线y2=8x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足．若直线AF的斜率为$-\sqrt{3}$，则|PF|=（ ）
| A． | $4\sqrt{3}$ | B． | 6 | C． | 8 | D． | 16 |
如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，E为AD的中点，PA⊥AD，BE∥CD，BE⊥AD，PA=AE=BE=2，CD=1．
19．在△ABC中，内角A，B，C所对的边分别为a，b，c，若a=$\sqrt{3}$，A=60°，B=45°，则b的长为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | 2 |
6．若实数a，b，c满足1＜b＜a＜2，0＜c＜$\frac{1}{8}$，则关于x的方程ax2+bx+c=0（ ）
| A． | 在区间（-1，0）内没有实数根 | |
| B． | 在区间（-1，0）内有一个实数根，在（-1，0）外有一个实数根 | |
| C． | 在区间（-1，0）内有两个相等的实数根 | |
| D． | 在区间（-1，0）内有两个不相等的实数根 |
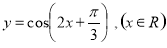的图像，只需把函数
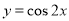的图像
个单位
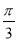个单位