题目内容
已知点A(-1,-1),B(3,1),直线l过点C(0,
),且与AB平行,求直线l的方程.
| 5 |
| 2 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:利用点斜式方程求解.
解答:
解:由已知,直线AB的斜率k=
=
.…(3分)
因为l∥AB,所以直线l的斜率为
.…(5分)
点C的坐标是(0,
).…(6分)
由点斜式直线l的方程是 y-
=
(x-0),…(10分)
即x-2y+5=0.…(12分)
| 1+1 |
| 3+1 |
| 1 |
| 2 |
因为l∥AB,所以直线l的斜率为
| 1 |
| 2 |
点C的坐标是(0,
| 5 |
| 2 |
由点斜式直线l的方程是 y-
| 5 |
| 2 |
| 1 |
| 2 |
即x-2y+5=0.…(12分)
点评:本题考查直线方程的求法,是基础题,解题时要注意直线间位置关系的合理运用.

练习册系列答案
相关题目
在区间[-
,
]上随机取一个数x,则事件“0≤sinx≤1”发生的概率为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
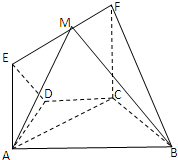 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.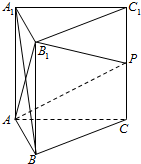 如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.
如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.