题目内容
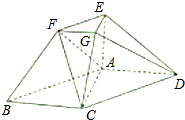 在如图所示的几何体中,ABCD为平行四边形,∠ACB=
在如图所示的几何体中,ABCD为平行四边形,∠ACB=| π |
| 2 |
(1)在线段AD上是否存在点M,使GM∥平面ABFE?并说明理由;
(2)若AC=BC=2AE,求二面角A-BF-C的大小.
考点:二面角的平面角及求法,直线与平面平行的性质
专题:空间位置关系与距离,空间角
分析:(1)存在点M,且点M是线段AD的中点.由已知条件推导出∠EGF=90°,BC=2FG,连结AF,得到四边形AFGM为平行四边形,由此能证明GM∥平面ABFE.
(2)分别以AC,AD,AE所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A-BF-C的大小.
(2)分别以AC,AD,AE所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A-BF-C的大小.
解答:
解:(1)存在点M,且点M是线段AD的中点,
∵EF∥AB,FG∥BC,EG∥AC,∠ACB=
,
∴∠EGF=90°,且△ABC∽△EFG,
∵AB=2EF,∴BC=2FG,
连结AF,∵FG∥BC,FG=
BC,
在平行四边形ABCD中,点M是线段AD的中点,
∴AM∥BC,且AM=
BC,∴FG∥AM,且FG=AM,
∴四边形AFGM为平行四边形,∴GM∥FA,
又∵FA?平面ABFE,GM不包含于平面ABFE,
∴GM∥平面ABFE.
(2)∵∠ACB=90°,∴∠CAD=90°,
又EA⊥平面ABCD,∴AC、AD、AE两两垂直,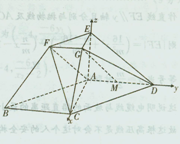
分别以AC,AD,AE所在直线为x轴,y轴,z轴,
建立空间直角坐标系,
设AC=BC=2AE=2,由题意得A(0,0,0),B(2,-2,0),
C(2,0,0),E(0,0,1),
∴
=(2,-2,0),
=(0,2,0),
又
=
,∴F(1,-1,1),
=(-1,1,1),
设平面BFC的法向量为
=(x1,y1,z1),
则
•
=0,
•
=0,
∴
,取x1=1,得
=(1,0,1),
设平面ABF的法向量为
=(x,y,z),
mj
•
=0,
•
=0,
∴
,取x=1,得
=(1,1,0),
∴cos<
,
>=
=
,
∴二面角A-BF-C的大小为
.
∵EF∥AB,FG∥BC,EG∥AC,∠ACB=
| π |
| 2 |
∴∠EGF=90°,且△ABC∽△EFG,
∵AB=2EF,∴BC=2FG,
连结AF,∵FG∥BC,FG=
| 1 |
| 2 |
在平行四边形ABCD中,点M是线段AD的中点,
∴AM∥BC,且AM=
| 1 |
| 2 |
∴四边形AFGM为平行四边形,∴GM∥FA,
又∵FA?平面ABFE,GM不包含于平面ABFE,
∴GM∥平面ABFE.
(2)∵∠ACB=90°,∴∠CAD=90°,
又EA⊥平面ABCD,∴AC、AD、AE两两垂直,

分别以AC,AD,AE所在直线为x轴,y轴,z轴,
建立空间直角坐标系,
设AC=BC=2AE=2,由题意得A(0,0,0),B(2,-2,0),
C(2,0,0),E(0,0,1),
∴
| AB |
| BC |
又
| EF |
| 1 |
| 2 |
| AB |
| BF |
设平面BFC的法向量为
| m |
则
| m |
| BC |
| m |
| BF |
∴
|
| m |
设平面ABF的法向量为
| n |
mj
| n |
| AB |
. |
| n |
| BF |
∴
|
| n |
∴cos<
| m |
| n |
| 1 | ||||
|
| 1 |
| 2 |
∴二面角A-BF-C的大小为
| π |
| 3 |
点评:本题考查直线与平面平行的证明,考查二面角大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
定义“D”:△f(x)=f(x+1)-f(x),△2f(x)=△[△f(x)],△3f(x)=△[△2f(x)],…,比如f(x)=x2,则有△f(x)=2x+1,△2f(x)=2,现已知f(x)=x2011,则△2012f(x)=( )
| A、1×2×3×…×2011 |
| B、1×2×3×…×2012 |
| C、2012 |
| D、0 |