题目内容
9.已知函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{6}$个单位后关于y轴对称,则函数f(x)的一个单调递增区间是( )| A. | $[{-\frac{5π}{6},\frac{π}{12}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{π}{6},\frac{π}{3}}]$ | D. | $[{\frac{π}{6},\frac{2π}{3}}]$ |
分析 由条件利用y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性,求得φ值,利用正弦函数的单调性可求单调递增区间.
解答 解:函数f(x)的图象向左平移$\frac{π}{6}$个单位后的函数解析式为:y=sin[2(x+$\frac{π}{6}$)+φ]=sin(2x+φ+$\frac{π}{3}$),
由函数图象关于y轴对称,可得:$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,即φ=kπ+$\frac{π}{6}$,k∈z,
由于|φ|<$\frac{π}{2}$,可得:φ=$\frac{π}{6}$,
可得:f(x)=sin(2x+$\frac{π}{6}$),
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解答:kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
可得,当k=1时,函数f(x)的一个单调递增区间是:[-$\frac{π}{3}$,$\frac{π}{6}$].
故选:B.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性、余弦函数的图象的对称性,属于基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
19.如图所示是y=Asin(ωx+φ)(A>0,ω>0)的图象的一段,它的一个解析式为( ) 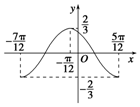

| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
17.为了得到函数y=sin2x+cos2x的图象,可以将函数y=cos2x-sin2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
19.已知平面向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a•({\overrightarrow a+\overrightarrow b})=3$,且$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$,则向量$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |