题目内容
18.设a∈R,函数$f(x)=\frac{{{2^x}+a}}{{{2^x}+1}}$;(1)求a的值,使得f(x)为奇函数;
(2)若$f(x)<\frac{a+2}{2}$对任意x∈R成立,求a的取值范围.
分析 (1)由f(x)在R上为奇函数,可得f(0)=0,解方程可得a的值,检验即可;
(2)由题意可得即为$\frac{{2}^{x}+a}{{2}^{x}+1}$<$\frac{a+2}{2}$恒成立,等价为$\frac{a-1}{{2}^{x}+1}$<$\frac{a}{2}$,即有2(a-1)<a(2x+1),讨论a=0,a>0,a<0,由参数分离,求得右边的范围,运用恒成立思想即可得到a的范围.
解答 解:(1)由f(x)的定义域为R,
且f(x)为奇函数,可得f(0)=0,
即有$\frac{1+a}{2}$=0,解得a=-1.
则f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-f(x),
则a=-1满足题意;
(2)$f(x)<\frac{a+2}{2}$对任意x∈R成立,
即为$\frac{{2}^{x}+a}{{2}^{x}+1}$<$\frac{a+2}{2}$恒成立,
等价为$\frac{a-1}{{2}^{x}+1}$<$\frac{a}{2}$,
即有2(a-1)<a(2x+1),
当a=0时,-1<0恒成立;
当a>0时,$\frac{2(a-1)}{a}$<2x+1,
由2x+1>1,可得$\frac{2(a-1)}{a}$≤1,
解得0<a≤2;
当a<0时,$\frac{2(a-1)}{a}$>2x+1不恒成立.
综上可得,a的取值范围是[0,2].
点评 本题考查函数的奇偶性的运用:求参数的值,考查不等式恒成立问题的解法,注意运用分类讨论和参数分离的思想方法,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{6}$个单位后关于y轴对称,则函数f(x)的一个单调递增区间是( )
| A. | $[{-\frac{5π}{6},\frac{π}{12}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{π}{6},\frac{π}{3}}]$ | D. | $[{\frac{π}{6},\frac{2π}{3}}]$ |
10.函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(-t)+4034t+2017,则实数t的取值范围是( )
| A. | $({-\frac{1}{2},+∞})$ | B. | $({-\frac{3}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{3}{2}})$ |

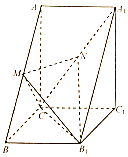 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=2,M、N分别是AB、A1C的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=2,M、N分别是AB、A1C的中点.