题目内容
14.设抛物线y2=4x的焦点为F,过点F作直线l与抛物线分别交于两点A,B,若点M满足$\overrightarrow{OM}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为3.分析 根据已知条件M是AB中点,设出A和B的坐标及直线方程,并将直线方程代入椭圆方程得到关于x的一元二次方程,利用根与系数的关系,表示出x1+x2和x1•x2,并求出P点坐标,根据|PF|=2,求得k的值,即可求得M点的横坐标.
解答 解:由题意可知:抛物线y2=4x的焦点为F,准线为x=-1,M是AB的中点,
设A(x1,y2),B(x2,y2),直线AB的方程为y=k(x-1),
将直线方程代入抛物线方程消去y得:k2x2-(2k2+4)+k2=0,
由根与系数的关系:x1+x2=2+$\frac{4}{{k}^{2}}$,x1•x2=1,
又设P(x0,y0),y0=$\frac{1}{2}$(y1+y2)=$\frac{1}{2}$[k(x1-1)+k(x2-1)]=$\frac{2}{k}$,
∴x0=$\frac{1}{{k}^{2}}$,
∴P($\frac{1}{{k}^{2}}$,$\frac{2}{k}$),
|PF|=x0+1=$\frac{1}{{k}^{2}}$+1=2,
∴k2=1,
∴M点的横坐标为3,
故答案为:3.
点评 本题考查抛物线的性质和应用及根与系数的关系,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,积累解题方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.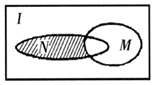 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
5.已知△ABC,$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$,AD与CE的交点为G,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,若$\overrightarrow{BG}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$,则λ+μ=( )
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
9.已知函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{6}$个单位后关于y轴对称,则函数f(x)的一个单调递增区间是( )
| A. | $[{-\frac{5π}{6},\frac{π}{12}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{π}{6},\frac{π}{3}}]$ | D. | $[{\frac{π}{6},\frac{2π}{3}}]$ |