题目内容
19.如图所示是y=Asin(ωx+φ)(A>0,ω>0)的图象的一段,它的一个解析式为( )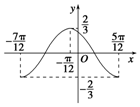
| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
分析 根据图象的最高点和最低点求出A,根据周期T=$\frac{5π}{12}-(-\frac{7π}{12})$求ω,图象过($-\frac{π}{12},\frac{2}{3}$),代入求φ,即可求函数f(x)的解析式;
解答 解:由图象的最高点$\frac{2}{3}$,最低点-$\frac{2}{3}$可得A=$\frac{2}{3}$,
周期T=$\frac{5π}{12}-(-\frac{7π}{12})$=π,
∴$ω=\frac{2π}{T}=2$.
图象过($-\frac{π}{12},\frac{2}{3}$),
∴$\frac{2}{3}=\frac{2}{3}Sin(2×-\frac{π}{12}+φ)$,
可得:φ=$2kπ+\frac{2π}{3}$.
则解析式为y=$\frac{2}{3}$sin(2x+$\frac{2π}{3}+2kπ$)=$\frac{2}{3}sin(2x+\frac{2π}{3})$
故选:D.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
14.如图,该程序运行后输出的结果是( )


| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
4.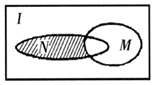 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
9.已知函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{6}$个单位后关于y轴对称,则函数f(x)的一个单调递增区间是( )
| A. | $[{-\frac{5π}{6},\frac{π}{12}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{π}{6},\frac{π}{3}}]$ | D. | $[{\frac{π}{6},\frac{2π}{3}}]$ |
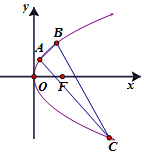 给定直线l:y=2x-16,抛物线G:y2=ax(a>0)
给定直线l:y=2x-16,抛物线G:y2=ax(a>0)