题目内容
已知箱子里装有4张大小、形状都相同的卡片,标号分别为1,2,3,4.
(Ⅰ)从箱子中任取两张卡片,求两张卡片的标号之和不小于5的概率;
(Ⅱ)从箱子中任意取出一张卡片,记下它的标号m,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号n,求使得幂函数f(x)=(m-n)2x
图象关于y轴对称的概率.
(Ⅰ)从箱子中任取两张卡片,求两张卡片的标号之和不小于5的概率;
(Ⅱ)从箱子中任意取出一张卡片,记下它的标号m,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号n,求使得幂函数f(x)=(m-n)2x
| m |
| n |
考点:古典概型及其概率计算公式,等可能事件的概率
专题:概率与统计
分析:(1)列出从箱子中任取两张卡片的所有基本事件,再求两张卡片的标号之和不小于5的基本事件的种数,利用古典概率求得,
(2)列出从箱子中任取两张卡片的所有基本事件,再求使得幂函数f(x)=(m-n)2x
图象关于y轴对称的基本事件,利用古典概率求得.
(2)列出从箱子中任取两张卡片的所有基本事件,再求使得幂函数f(x)=(m-n)2x
| m |
| n |
解答:
解:(1)从箱子中任取两张卡片的所有基本事件有:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共有6种,
其中两张卡片的标号之和不小于5的基本事件有(1,4)(2,4),(3,4),(2,3)共4种,故两张卡片的标号之和不小于5的概率P=
=
;
(2)从箱子中任取两张卡片的所有基本事件有:(1,2),(2,1),(1,3),(3,1),(1,4),(4,1),(2,3),(3,2),(2,4),(4,2),(3,4),(4,3),(1,1),(2,2),(3,3),(4,4)共16种,
使得幂函数f(x)=(m-n)2x
图象关于y轴对称的基本事件有:(2,1),(1,4),(4,1),(2,3),(4,2)共5种,
所以使得幂函数f(x)=(m-n)2x
图象关于y轴对称的概率P=
.
其中两张卡片的标号之和不小于5的基本事件有(1,4)(2,4),(3,4),(2,3)共4种,故两张卡片的标号之和不小于5的概率P=
| 4 |
| 6 |
| 2 |
| 3 |
(2)从箱子中任取两张卡片的所有基本事件有:(1,2),(2,1),(1,3),(3,1),(1,4),(4,1),(2,3),(3,2),(2,4),(4,2),(3,4),(4,3),(1,1),(2,2),(3,3),(4,4)共16种,
使得幂函数f(x)=(m-n)2x
| m |
| n |
所以使得幂函数f(x)=(m-n)2x
| m |
| n |
| 5 |
| 16 |
点评:本题主要考查了古典概率问题,关键是要把所有的事件都要不重不漏的一一列举出来.

练习册系列答案
相关题目
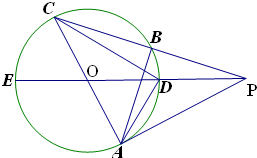 如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.
如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.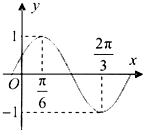 已知函数f(x)=sin(ωx+φ)(ω>0,φ<
已知函数f(x)=sin(ωx+φ)(ω>0,φ<