题目内容
某中学在高三年级开设了A、B、C三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从A、B、C三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人):
(1)求x、y的值;
(2)若从A、B两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自同一兴趣小组的概率.
| 兴趣小组 | 小组人数 | 抽取人数 |
| A | 24 | x |
| B | 36 | 3 |
| C | 48 | y |
(2)若从A、B两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自同一兴趣小组的概率.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(1)根据题意,由分层抽样的特点,可得
=
=
,解可得答案;
(2)记从兴趣小组A中抽取的2人为a1,a2,从兴趣小组B中抽取的3人为b1,b2,b3,设选中的2人都来自兴趣小组B的事件为E,用列举法可得从5人中选2人作发言的基本事件的数目,同时可得E包含的基本事件的数目,由等可能事件的概率公式,计算可得答案.
| x |
| 24 |
| 3 |
| 36 |
| y |
| 48 |
(2)记从兴趣小组A中抽取的2人为a1,a2,从兴趣小组B中抽取的3人为b1,b2,b3,设选中的2人都来自兴趣小组B的事件为E,用列举法可得从5人中选2人作发言的基本事件的数目,同时可得E包含的基本事件的数目,由等可能事件的概率公式,计算可得答案.
解答:
解:(1)由题意可得,
=
=
,
解得x=2,y=4.
(2)记从兴趣小组A中抽取的2人为a1,a2,
从兴趣小组B中抽取的3人为b1,b2,b3,
则从兴趣小组A,B抽取的5人中选2人作专题发言的基本事件有:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),
(a2,b1),(a2,b2),(a2,b3),(b1,b2),
(b1,b3),(b2,b3)共10种.
设选中的2人都来自同一兴趣小组的事件为E,
则E包含的基本事件有:
(a1,a2),(b1,b2),(b1,b3),(b2,b3)共4种.
所以P(E)=
=
;
故选中的2人都来自同一兴趣小组的概率为
.
| x |
| 24 |
| 3 |
| 36 |
| y |
| 48 |
解得x=2,y=4.
(2)记从兴趣小组A中抽取的2人为a1,a2,
从兴趣小组B中抽取的3人为b1,b2,b3,
则从兴趣小组A,B抽取的5人中选2人作专题发言的基本事件有:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),
(a2,b1),(a2,b2),(a2,b3),(b1,b2),
(b1,b3),(b2,b3)共10种.
设选中的2人都来自同一兴趣小组的事件为E,
则E包含的基本事件有:
(a1,a2),(b1,b2),(b1,b3),(b2,b3)共4种.
所以P(E)=
| 4 |
| 10 |
| 2 |
| 5 |
故选中的2人都来自同一兴趣小组的概率为
| 2 |
| 5 |
点评:此题考查了古典概型概率计算公式,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

练习册系列答案
相关题目
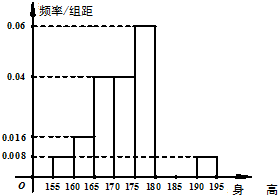 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.