题目内容
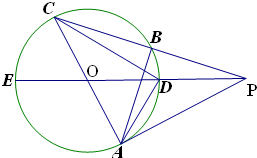如图，PA是⊙O的切线，PE过圆心0，AC为⊙O的直径，PC与⊙O相交于B、C两点，连接AB、CD．（Ⅰ）求证：∠PAD=∠CDE；
（Ⅱ）求证：
| PA2 |
| PC•PE |
| BD |
| AD |
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（Ⅰ）利用圆的切线的性质，结合等腰三角形的性质，即可证明∠PAD=∠CDE；
（Ⅱ）利用△PBD∽△PEC，结合切割线定理即可证明结论．
（Ⅱ）利用△PBD∽△PEC，结合切割线定理即可证明结论．
解答：
（Ⅰ）解：由PA是圆O的切线，因此∠PAD=∠ACD，…（2分）
在等腰△OCD中，OD=OC，
可得∠ACD=∠CDE，…（4分）
所以∠PAD=∠CDE．…（5分）
（Ⅱ）证明：连接EC
∵△PBD∽△PEC，
∴
=
，…（7分）
由切割线定理可知，PA2=PB•PC，
则PB=
，…（9分）
又EC=AD，可得：
=
．…（10分）
（Ⅰ）解：由PA是圆O的切线，因此∠PAD=∠ACD，…（2分）在等腰△OCD中，OD=OC，
可得∠ACD=∠CDE，…（4分）
所以∠PAD=∠CDE．…（5分）
（Ⅱ）证明：连接EC
∵△PBD∽△PEC，
∴
| PB |
| PE |
| BD |
| CE |
由切割线定理可知，PA2=PB•PC，
则PB=
| PA2 |
| PC |
又EC=AD，可得：
| PA2 |
| PC•PE |
| BD |
| AD |
点评：本题考查与圆有关的比例线段，考查切割线定理，属于中档题．
练习册系列答案
相关题目
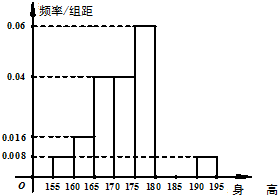从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．