题目内容
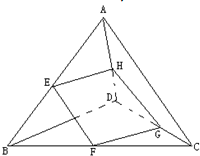 已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.
已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:利用三角形的中位线定理、平行四边形的判定定理可得:四边形EFGH是平行四边形.由EH∥BD,EF∥AC,BD⊥AC,可得EF⊥EH.即可证明平行四边形EFGH是矩形.
解答:
证明:∵E、F分别是空间四边形四条边AB、BC的中点,
∴EF∥AC,EF=
AC.
同理可得GH∥AC.∴EF
GH.
∴四边形EFGH是平行四边形.
可得EH∥BD,又BD⊥AC,
∴EF⊥EH.
∴平行四边形EFGH是矩形.
∴EF∥AC,EF=
| 1 |
| 2 |
同理可得GH∥AC.∴EF
| ∥ |
. |
| 1 |
| 2 |
∴四边形EFGH是平行四边形.
可得EH∥BD,又BD⊥AC,
∴EF⊥EH.
∴平行四边形EFGH是矩形.
点评:本题考查了三角形的中位线定理、平行四边形的判定、矩形的判定定理、异面直线所成的角,考查了推理能力,属于基础题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
已知集合A={x∈R|0<x<1},B={x∈R|(2x-1)(x+1)≤0},则(∁RA)∩B( )
A、[0,
| ||
| B、[-1,0] | ||
C、[
| ||
| D、(-∞,-1]∪[0,+∞) |
在△ABC中,|AC|2=
•
,
=(-2,-3),
=(m,1),则m的值等于( )
| BC |
| AC |
| BA |
| BC |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
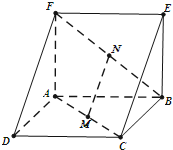 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.