题目内容
 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.(1)求证:面PAB⊥面PAC;
(2)求证:PB∥平面AEC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:对第(1)问,先证平面PAC内的一条直线AC⊥平面PAB,再由面面垂直的判定定理得证.
对第(2)问,先连结BD交AC于点O,连结EO,再证直线PB平行于平面AEC内的直线EO,从而由线面平行的判断定理得证.
对第(2)问,先连结BD交AC于点O,连结EO,再证直线PB平行于平面AEC内的直线EO,从而由线面平行的判断定理得证.
解答:
证明:(1)∵PA⊥平面ABCD,AC?平面ABCD,∴PA⊥AC.又AB⊥AC,PA∩AB=A,
∴AC⊥平面PAB,∴面PAC⊥面PAB.
(2)如下图所示, 连结BD交AC于点O,连结EO,则EO是△PDB的中位线,∴EO∥PB.
连结BD交AC于点O,连结EO,则EO是△PDB的中位线,∴EO∥PB.
又EO?平面AEC,PB?平面AEC,∴PB∥平面AEC.
∴AC⊥平面PAB,∴面PAC⊥面PAB.
(2)如下图所示,
 连结BD交AC于点O,连结EO,则EO是△PDB的中位线,∴EO∥PB.
连结BD交AC于点O,连结EO,则EO是△PDB的中位线,∴EO∥PB.又EO?平面AEC,PB?平面AEC,∴PB∥平面AEC.
点评:本题考查了线面平行的判定定理和面面垂直的判定定理,证线面平行的关键是在已知平面内找一条直线与已知直线平行;证面面垂直的关键是在其中一个平面内寻找一条直线与另一个平面垂直.

练习册系列答案
相关题目
已知集合M={(x,y)|y2=x+1},下列关系式中正确的是( )
| A、-1,0∈M |
| B、{-1,0}∈M |
| C、(-1,0)∈M |
| D、(-1,0)∉M |
下列命题中正确的是( )
| A、若a>b,则ac2>bc2 | ||||
B、若a>b,c<d,则
| ||||
| C、若a>b,c>d,则a-c>b-d | ||||
D、若ab>0,a>b,则
|
已知向量
=(1,-n),
=(2,n),若
•
=1,则实数n=( )
| a |
| b |
| a |
| b |
| A、1或-1 | B、-1 | C、0 | D、-2 |

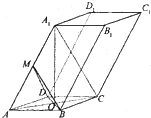 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形,AC∩BD=O,AA1=2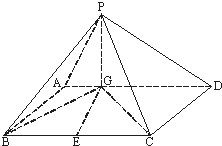 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=