题目内容

正方体的棱长为2，则以各面的中心为顶点的凸多面体的体积是
 
．
考点：棱柱、棱锥、棱台的体积
专题：
分析：正方体各个面的中心为顶点的凸多面体为正八面体，棱长为a=
2
，高为h=2，由此能求出凸多面体的体积．
解答： 解：正方体各个面的中心为顶点的凸多面体为正八面体，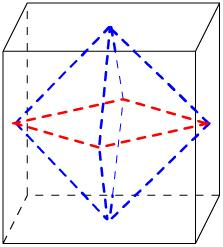
棱长为a=
2
，高为h=2，
从而V=
1
3
a2h=
4
3
．
故答案为：
4
3
．
点评：本题考查凸多面体的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
若函数f（x）=
cosx
cos(
π
6
-x)
，则f（
π
180
）+f（
π
90
）+f（
π
60
）+f（
π
45
）+f（
π
36
）+…+f（
59π
180
）=
 
．
已知函数y=f（x）是R上的偶函数，对于x∈R都有f（x+6）=f（x）+f（3）成立，当x1，x2∈[0，3]，且x1≠x2时，都有
f(x1)-f(x2)
x1-x2
＞0．给出下列命题：
①f（-3）=0；
②直线x=-6是函数y=f（x）的图象的一条对称轴；
③函数y=f（x）在[-9，-6]上为增函数；
④函数y=f（x）在[-9，9]上有四个零点．
其中所有正确命题的序号为
 
．（把所有正确命题的序号都填上）．
某同学在高考报志愿时，报了4所符合自己分数和意向的高校，若每一所学校录取的概率为
1
2
，则这位同学被其中一所学校录取的概率为
 
．
函数y=xe-x，x∈[0，4]的最大值是
 
．
已知函数f（x）是偶函数，且当x≥0时，f（x）=-（x-1）2+1，若f（f（a））=
1
2
，则a=
 
．
从8人中选出5人从事五项不同的工作，其中甲、乙两人都不能从事第一项和第三项工作，则不同的分配方法有
 
种．
已知直线l1：ax-y+2a=0，l2：（2a-1）x+ay+a=0互相垂直，则a的值是（　　）
A、0B、1C、0或1D、0或-1
已知正三角形ABC的边长为2a，那么△ABC的直观图△A′B′C′的面积为（　　）
A、
3
4
a2
B、
3
2
a2
C、
6
2
a2
D、
6
4
a2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网