Question

已知函数f（x）是偶函数，且当x≥0时，f（x）=-（x-1）²+1，若f（f（a））=

1

2

，则a=

 

．

Answer 1

考点：函数奇偶性的性质

专题：函数的性质及应用

分析：函数f（x）是偶函数，且当x≥0时，f（x）=-（x-1）²+1，可得：当x＜0时，f（x）=f（-x）
=-（x+1）²+1．于是f（x）≤1．如图所示．对f（a）分类讨论：当f（a）＞0时，由-（f（a）-1）²+1=

1

2

解出f（a），再解出a即可；f（a）=0直接验证；若f（a）＜0时，同理可得．

解答： 解：∵函数f（x）是偶函数，且当x≥0时，f（x）=-（x-1）²+1，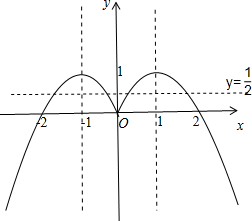
∴当x＜0时，f（x）=f（-x）=-（x+1）²+1．
∴f（x）=

-x2+2x，x≥0 -x2-2x，x＜0

，可知f（x）≤1．
如图所示．
若f（a）＞0时，由-（f（a）-1）²+1=

1

2

，
解得f（a）=

2- 2

2

，或f（a）=

2+ 2

2

（舍去）
∴-（a-1）²+1=

2- 2

2

，或-(a+1)2+1=

2- 2

2

，
解得a=

2± 2 2

2

，a=

-2± 2 2

2

．
当f（a）=0时，a=±2，0，但是f（0）=0≠

1

2

，应该舍去．
若f（a）＜0时，由-（f（a）-1）²+1=

1

2

，解得f（a）=

2- 2

2

＞0，或f（a）=

2+ 2

2

＞0，舍去．
综上可得：a=

2± 2 2

2

，a=

-2± 2 2

2

．
故答案为：

2± 2 2

2

，

-2± 2 2

2

．

点评：本题考查了二次函数的图象与性质、函数奇偶性、复合函数的性质，考查了分类讨论的思想方法，考查了推理能力与计算能力，属于难题．