题目内容

19．过抛物线y2=2x焦点的直线交抛物线于A，B两点，若AB的中点M到该抛物线准线的距离为5，则线段AB的长度为10．

分析 利用抛物线的简单性质以及抛物线的定义转化求解即可．

解答 解：过抛物线y2=2x焦点的直线交抛物线于A，B两点，若AB的中点M到该抛物线准线的距离为5，A到准线的距离与B到准线的距离的和是10，
由抛物线的定义可知AB=10，
故答案为：10．

点评 本题考查抛物线的基础知识，抛物线简单性质的应用，是简单题．

练习册系列答案
相关题目
9．已知P：?x＞0，lnx＜x，则￢P为（　　）
A．?x≤0，lnx0＞x0B．?x≤0，lnx0≥x0C．?x＞0，lnx0≥x0D．?x＞0，lnx0＜x0
10．已知实数x，y满足$\left\{\begin{array}{l}x+y≤6\\ x-y≤2\\ x≥0\\ y≥0\end{array}\right.$则z=2x+y的最大值是10．
7．已知全集U=R，A={x|x2-2x＜0}，B={x|x≥1}，则A∪（∁UB）=（　　）
A．（0，+∞）B．（-∞，1）C．（-∞，2）D．（0，1）
14．已知实数a，b满足0＜a＜1，-1＜b＜1，则函数$y=\frac{1}{3}a{x^3}+a{x^2}+b$有三个零点的概率为$\frac{5}{16}$．
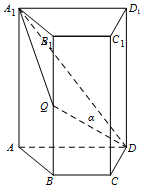4．如图，四棱柱ABCD-A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，Q为BB1的中点，过A1，Q，D三点的平面记为α．
（Ⅰ）证明：平面α与平面A1B1C1D1的交线平行于直线CD；
（Ⅱ）若AA1=3，BC=CD=$\sqrt{3}$，∠BCD=120°，求平面α与底面ABCD所成二面角的大小．
11．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，M为C上除长轴顶点外的一动点，以M为圆心，$\frac{{\sqrt{2}}}{2}$为半径作圆，过原点O作圆M的两条切线，A、B为切点，当M为短轴顶点时∠AOB=$\frac{π}{2}$．
（Ⅰ）求椭圆的方程；
（Ⅱ）设椭圆的右焦点为F，过点F作MF的垂线交直线x=$\sqrt{2}$a于N点，判断直线MN与椭圆的位置关系．
8．下面四个命题中，真命题是（　　）
①从匀速传递的产品生产流水线上，质检员每30分钟从生产流水线中抽取一件产品进行某项指标检测，这样的抽样方法是系统抽样；
②两个变量的线性相关程度越强，则相关系数的值越接近于1；
③两个分类变量X与Y的观测值κ2，若κ2越小，则说明“X与Y有关系”的把握程度越大；
④随机变量X～N（0，1），则P（|X|＜1）=2P（X＜1）-1．
A．①④B．②④C．①③D．②③
9．若复数$z=\frac{1+ai}{2-i}$（i是虚数单位）为纯虚数，则实数a的值为（　　）
A．2B．$\frac{1}{2}$C．$-\frac{1}{2}$D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网