Question

4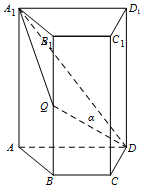．如图，四棱柱ABCD-A₁B₁C₁D₁中，A₁A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，Q为BB₁的中点，过A₁，Q，D三点的平面记为α．
（Ⅰ）证明：平面α与平面A₁B₁C₁D₁的交线平行于直线CD；
（Ⅱ）若AA₁=3，BC=CD=$\sqrt{3}$，∠BCD=120°，求平面α与底面ABCD所成二面角的大小．

Answer 1

分析 （Ⅰ）延长AB，DC交于点P，由已知可得AD∥BC，且AD=2BC，则AB=BP，得到A₁，Q，P三点共线，此时平面α与平面ABCD的交线为CD，再由面面平行的性质可得平面α与平面A₁B₁C₁D₁的交线平行于直线CD；
（Ⅱ）在梯形ABCD中，由已知求得ABCD是等腰梯形，进一步得到△ADP为等边三角形，连接AC、A₁C，则AC⊥CD，可得∠A₁CA就是平面α与底面ABCD所成二面角的平面角，在直角△A₁CA中，求得$∠{A_1}CA=\frac{π}{4}$，即平面α与底面ABCD所成二面角的大小为$\frac{π}{4}$．

解答 （Ⅰ）证明：如图，延长AB，DC交于点P，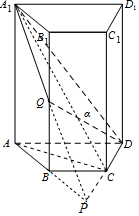
∵AD∥BC，且AD=2BC，∴AB=BP，
又∵Q为BB₁ 的中点，
∴A₁，Q，P三点共线，此时平面α与平面ABCD的交线为CD，
又平面ABCD∥平面A₁B₁C₁D₁，根据面面平行的性质定理可得，
平面α与平面A₁B₁C₁D₁的交线平行于直线CD；
（Ⅱ）解：在梯形ABCD中，∵BC=CD=$\sqrt{3}$，∠BCD=120°，
∴BD=3，$AD=2\sqrt{3}$，$∠ADB=\frac{π}{6}$，得$AB=\sqrt{3}$，$∠DAB=\frac{π}{3}$，
说明梯形ABCD是等腰梯形，
∴AC=BD=3，
可知△ADP为等边三角形，连接AC、A₁C，则AC⊥CD，
又AA₁⊥CD，∴CD⊥平面AA₁C，
此时∠A₁CA就是平面α与底面ABCD所成二面角的平面角，
在直角△A₁CA中，AC=AA₁=3，∴$∠{A_1}CA=\frac{π}{4}$，
即平面α与底面ABCD所成二面角的大小为$\frac{π}{4}$．

点评 本题考查空间几何体的线面位置关系，空间想象能力，空间角的计算问题，是中档题．