题目内容
已知二次函数f(x)=ax2+bx+c(a≠0),其图象关于直线x=1对称,f(2)=0,且方程f(x)=x有等根.
(1)求a、b、c的值;
(2)是否存在实数m,n(m<n=,使得函数f(x)在定义域[m,n]上的值域为[3m,3n].如果存在,求出m,n的值;如果不存在,请说明理由.
(1)求a、b、c的值;
(2)是否存在实数m,n(m<n=,使得函数f(x)在定义域[m,n]上的值域为[3m,3n].如果存在,求出m,n的值;如果不存在,请说明理由.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据题意得出f(2)=0,f(0)=0,设f(x)=ax(x-2)=ax2-2ax,利用f(x)=x有等根.求解即可.
(2))f(x)=-
x2+x=-
(x-1)2+
≤
,根据f(x)在[m,n]上为增函数得出f(m)=3m,f(n)=3n,求解即可.
(2))f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵二次函数f(x)=ax2+bx+c(a≠0),
其图象关于直线x=1对称,f(2)=0,
∴f(0)=0
∴f(x)=ax(x-2)=ax2-2ax,
∵方程f(x)=x有等根.
∴ax2=(2a+1)x,
2a+1=0
a=-
,
∴f(x)=-
x2+x,
a=-
,b=1,c=0,
(2)f(x)=-
x2+x=-
(x-1)2+
≤
∵m<n≤
∴f(x)在[m,n]上为增函数
∵f(m)=3m,f(n)=3n
∴m=-4,n=0(m=0,n=-4,不合题意,舍去)
∴存在m=-4,n=0
其图象关于直线x=1对称,f(2)=0,
∴f(0)=0
∴f(x)=ax(x-2)=ax2-2ax,
∵方程f(x)=x有等根.
∴ax2=(2a+1)x,
2a+1=0
a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
a=-
| 1 |
| 2 |
(2)f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵m<n≤
| 1 |
| 6 |
∴f(x)在[m,n]上为增函数
∵f(m)=3m,f(n)=3n
∴m=-4,n=0(m=0,n=-4,不合题意,舍去)
∴存在m=-4,n=0
点评:本题考查了二次函数的性质,运用性质求解解析式,单调性运用求解值域问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
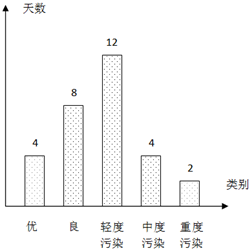 经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图:
经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图: