题目内容
已知函数f(x)对一切实数x,y都满足f(x+y)=f(y)+(x+2y+1)x,且f(1)=0,
(1)求f(0)的值;
(2)求f(x)的解析式;
(3)当x∈[0,
]时,f(x)+3<2x+a恒成立,求a的范围.
(1)求f(0)的值;
(2)求f(x)的解析式;
(3)当x∈[0,
| 1 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)利用赋值法,令x=1,y=0,可求得f(0);
(2)令y=0,代入f(x)=f(0)+(x+1)x,即可判断函数的解析式;
(3)f(x)+3<2x+a,得a>x2-x+1,构造函数y=x2-x+1,根据函数的单调性求出函数的在∈[0,
]的最大值,即可求出a 的范围,
(2)令y=0,代入f(x)=f(0)+(x+1)x,即可判断函数的解析式;
(3)f(x)+3<2x+a,得a>x2-x+1,构造函数y=x2-x+1,根据函数的单调性求出函数的在∈[0,
| 1 |
| 2 |
解答:
解:( 1)令x=1,y=0,则f(1)=f(0)+(1+1)×1,∴f(0)=f(1)-2=-2.
(2)令y=0,则f(x)=f(0)+(x+1)x,∴f(x)=x2+x-2.
(3)由f(x)+3<2x+a,得a>x2-x+1.设y=x2-x+1,则y=x2-x+1在(-∞,
]上是减函数,所以ymax=1,
从而可得a>1.
(2)令y=0,则f(x)=f(0)+(x+1)x,∴f(x)=x2+x-2.
(3)由f(x)+3<2x+a,得a>x2-x+1.设y=x2-x+1,则y=x2-x+1在(-∞,
| 1 |
| 2 |
从而可得a>1.
点评:本题考查抽象函数及其应用,考查函数奇偶性与单调性的综合,突出考查赋值法的应用,考查推理与运算能力,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
在等差数列{an}中,a1=2,a3+a5=10,则a7=( )
| A、5 | B、8 | C、10 | D、14 |
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
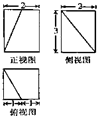

| A、9 | ||
| B、10 | ||
| C、11 | ||
D、
|
在△ABC中,三边a,b,c与面积S的关系是S=
,则∠C=( )
| a2+b2-c2 |
| 4 |
| A、30° | B、60° |
| C、45° | D、90° |
已知tanα=
,且点A(-4,a)在角α的终边上,则a的值是( )
| 3 |
A、4
| ||
B、-4
| ||
C、±4
| ||
D、
|
下列各组函数表示同一函数的是( )
A、f(x)=
| |||||
B、f(x)=
| |||||
| C、f(x)=1,g(x)=x0 | |||||
D、f(x)=x+1,g(x)=
|