题目内容
已知全集U=R,集合A={x|x2-4x+3<0},B={x|
>1},C={x|x-m|>2,m∈R}.对于任意x∈A∩B,总有x∈∁UC.
(1)A∩B;
(2)求实数m的取值范围.
| 2 |
| x-2 |
(1)A∩B;
(2)求实数m的取值范围.
考点:交集及其运算
专题:集合
分析:(1)利用交集定义能求出A∩B.
(2)由已知得CUC={x|m-2≤x≤m+2},
,由此能求出实数m的取值范围.
(2)由已知得CUC={x|m-2≤x≤m+2},
|
解答:
解:(1)∵全集U=R,集合A={x|x2-4x+3<0}={x|1<x<3},
B={x|
>1}={x|2<x<4},
∴A∩B={x|2<x<3}.
(2)∵C={x|x-m|>2,m∈R}={x|x>m+2或x<m-2}.
∴CUC={x|m-2≤x≤m+2},
∵对于任意x∈A∩B,总有x∈∁UC.
∴
,解得1≤m≤4.
∴实数m的取值范围是[1,4].
B={x|
| 2 |
| x-2 |
∴A∩B={x|2<x<3}.
(2)∵C={x|x-m|>2,m∈R}={x|x>m+2或x<m-2}.
∴CUC={x|m-2≤x≤m+2},
∵对于任意x∈A∩B,总有x∈∁UC.
∴
|
∴实数m的取值范围是[1,4].
点评:本题考查交集的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意交集性质的合理运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
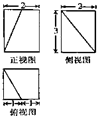
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )

| A、9 | ||
| B、10 | ||
| C、11 | ||
D、
|
在△ABC中,三边a,b,c与面积S的关系是S=
,则∠C=( )
| a2+b2-c2 |
| 4 |
| A、30° | B、60° |
| C、45° | D、90° |
已知tanα=
,且点A(-4,a)在角α的终边上,则a的值是( )
| 3 |
A、4
| ||
B、-4
| ||
C、±4
| ||
D、
|
 三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成的角等于
三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成的角等于