题目内容
用[x]表示不超过x的最大整数,如[0.78]=0,[3.01]=3,如果定义数列{xn}的通项公式为xn=[
](n∈N*),则x1+x2+…+x5n= .
| n |
| 5 |
考点:数列的函数特性,函数的概念及其构成要素
专题:等差数列与等比数列
分析:由于xn=[
](n∈N*),可得x1=x2=x3=x4=0,x5=x6=…=x9=1,…,x5n-5=x5n-4=…=x5n-1=n-1.x5n=n.因此x1+x2+…+x5n=0+5×1+5×2+…+5×(n-1)+n,利用等差数列的前n项和公式即可得出.
| n |
| 5 |
解答:
解:∵xn=[
](n∈N*),
∴x1=x2=x3=x4=0,x5=x6=…=x9=1,…,x5n-5=x5n-4=…=x5n-1=n-1.x5n=n.
∴x1+x2+…+x5n=0+5×1+5×2+…+5×(n-1)+n
=5×
+n
=
n2-
n.
故答案为:
n2-
n.
| n |
| 5 |
∴x1=x2=x3=x4=0,x5=x6=…=x9=1,…,x5n-5=x5n-4=…=x5n-1=n-1.x5n=n.
∴x1+x2+…+x5n=0+5×1+5×2+…+5×(n-1)+n
=5×
| n(n-1) |
| 2 |
=
| 5 |
| 2 |
| 3 |
| 2 |
故答案为:
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题考查了新定义、等差数列的前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
下列各组函数表示同一函数的是( )
A、f(x)=
| |||||
B、f(x)=
| |||||
| C、f(x)=1,g(x)=x0 | |||||
D、f(x)=x+1,g(x)=
|
若a>1,则函数y=(
)•ax的图象的基本形状是( )
| x |
| |x| |
A、 |
B、 |
C、 |
D、 |
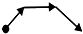
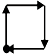
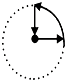
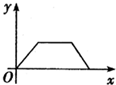 如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )
如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )