题目内容
设椭圆C:
+
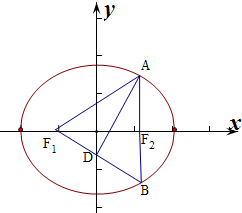
=1(a>b>0)的左右焦点分别为F1,F2,过F2作x轴的垂线与C相交于A,B两点,F1B与y轴相交于点D.若AD⊥F1B,则椭圆C的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据条件分别求出A,B,D的坐标,利用AD⊥F1B,建立方程关系即可得到结论
解答:
 解:不妨假设椭圆中的a=1,则F1(-c,0),F2(c,0),
解:不妨假设椭圆中的a=1,则F1(-c,0),F2(c,0),
当x=c时,由
+
=1得y=
=b2,即A(c,b2),
B(c,-b2),
设D(0,m),∵F1,D,B三点共线,
∴
=
,解得m=-
,即D(0,-
),
∴若AD⊥F1B,
则kAD•kF1B=-1,
即
•
=-1,
即3b4=4c2,
则
b2=2c=
(1-c2)=2c,
即
c2+2c-
=0,
解得c=
=
,
则c=
=
,
∵a=1,
∴离心率e=
=
,
故选B.
 解:不妨假设椭圆中的a=1,则F1(-c,0),F2(c,0),
解:不妨假设椭圆中的a=1,则F1(-c,0),F2(c,0),当x=c时,由
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
B(c,-b2),
设D(0,m),∵F1,D,B三点共线,
∴
| m |
| c |
| b2 |
| -2c |
| b2 |
| 2 |
| b2 |
| 2 |
∴若AD⊥F1B,
则kAD•kF1B=-1,
即
b2+
| ||
| c |
| -b2 |
| -c-c |
即3b4=4c2,
则
| 3 |
| 3 |
即
| 3 |
| 3 |
解得c=
-2±
| ||||||
2
|
| -2±4 | ||
2
|
则c=
| 2 | ||
2
|
| ||
| 3 |
∵a=1,
∴离心率e=
| c |
| a |
| ||
| 3 |
故选B.
点评:本题主要考查椭圆离心率的求解,根据条件求出对应点的坐标,利用直线垂直与斜率之间的关系是解决本题的关键,运算量较大.为了方便,可以先确定一个参数的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个空间几何体的三视图如图所示,则该几何体的表面积为( )


| A、48 | ||
B、32+8
| ||
C、48+8
| ||
| D、80 |
已知tanα=
,且点A(-4,a)在角α的终边上,则a的值是( )
| 3 |
A、4
| ||
B、-4
| ||
C、±4
| ||
D、
|