题目内容
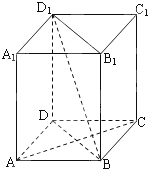 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=| 2 |
(1)求直线D1B与平面ABCD所成角的大小;
(2)求证:AC⊥平面BB1D1D.
考点:直线与平面垂直的判定,直线与平面所成的角
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)由D1D⊥平面ABCD,BD是D1B在底面ABCD上的射影,则∠D1BD是直线D1B与平面ABCD所成的角,在直角三角形D1BD中,由已知数据,即可求出∠D1BD;
(2)要证AC⊥平面BB1D1D,只需证得AC⊥BD,AC⊥D1D,由正方形的对角线的性质和D1D⊥底面ABCD,即可得证.
(2)要证AC⊥平面BB1D1D,只需证得AC⊥BD,AC⊥D1D,由正方形的对角线的性质和D1D⊥底面ABCD,即可得证.
解答:
(1) 解:∵D1D⊥平面ABCD,BD是D1B在底面ABCD上的射影,
解:∵D1D⊥平面ABCD,BD是D1B在底面ABCD上的射影,
∴∠D1BD是直线D1B与平面ABCD所成的角,
在直角三角形D1BD中,BD=
,D1D=
,
则tan∠D1BD=
=1,
∴∠D1BD=45°,
即直线D1B与平面ABCD所成角的大小为45°;
(2)证明:∵ABCD为正方形,∴AC⊥BD,
∵D1D⊥平面ABCD,∴D1D⊥AC,
又BD∩D1D=D,
∴AC⊥平面BB1D1D.
 解:∵D1D⊥平面ABCD,BD是D1B在底面ABCD上的射影,
解:∵D1D⊥平面ABCD,BD是D1B在底面ABCD上的射影,∴∠D1BD是直线D1B与平面ABCD所成的角,
在直角三角形D1BD中,BD=
| 2 |
| 2 |
则tan∠D1BD=
| D1D |
| BD |
∴∠D1BD=45°,
即直线D1B与平面ABCD所成角的大小为45°;
(2)证明:∵ABCD为正方形,∴AC⊥BD,
∵D1D⊥平面ABCD,∴D1D⊥AC,
又BD∩D1D=D,
∴AC⊥平面BB1D1D.
点评:本题考查空间直线与平面所成的角,考查直线与平面垂直的判定和性质,同时考查运算能力,属于中档题.

练习册系列答案
相关题目
函数y=sin2(
+x)-sin2(
-x)的值域是( )
| π |
| 4 |
| π |
| 4 |
| A、[-1,0] | ||
| B、[0,1] | ||
| C、[-1,1] | ||
D、[-
|
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.