题目内容
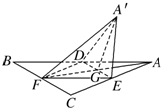如图，正三角形ABC的中线AF与中位线DE相交于点G，已知△A′ED是△AED绕DE旋转过程中的一个图形，现给出下列四个命题：①动点A′在平面ABC上的射影在线段AF上；
②恒有平面A′GF⊥平面BCED；
③三棱锥A′-FED的体积有最大值；
④直线A′E与BD不可能垂直．
其中正确的命题的序号是
考点：组合几何体的面积、体积问题
专题：空间位置关系与距离
分析：由斜线的射影定理可判断①正确；由面面垂直的判定定理，可判断②正确；由三棱锥的体积公式，可判断③正确；由异面直线所成的角的概念可判断④不正确．
解答：
解：∵A′D=A′E，△ABC是正三角形，∴A′在平面ABC上的射影在线段AF上，故①正确；
由①知，平面A′GF一定过平面BCED的垂线，根据面面垂直的判定定理可得：恒有平面A′GF⊥平面BCED，故②正确；
三棱锥A′-FED的底面积是定值，体积由高即A′到底面的距离决定，当平面A′DE⊥平面BCED时，三棱锥A′-FED的体积有最大值，故③正确；
当（A′E）2+EF2=（A′F）2时，面直线A′E与BD垂直，故④不正确；
故答案为：①②③．
由①知，平面A′GF一定过平面BCED的垂线，根据面面垂直的判定定理可得：恒有平面A′GF⊥平面BCED，故②正确；
三棱锥A′-FED的底面积是定值，体积由高即A′到底面的距离决定，当平面A′DE⊥平面BCED时，三棱锥A′-FED的体积有最大值，故③正确；
当（A′E）2+EF2=（A′F）2时，面直线A′E与BD垂直，故④不正确；
故答案为：①②③．
点评：本题考查了线面、面面垂直的判定定理、性质定理的运用，考查了空间线线、线面的位置关系及所成的角的概念，考查了空间想象能力，属基础题
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知命题p：“?x∈R，x2+1＞0”命题q：“?x∈R，tanx=2”，则下列判断正确的是（ ）
| A、p∨q为真，￢p为真 |
| B、p∨q为假，￢p为假 |
| C、p∧q为真，￢p为真 |
| D、p∧q为真，￢p为假 |
已知a＞1，logax＜logay＜0，则（ ）
| A、1＜x＜y |
| B、1＜y＜x |
| C、0＜x＜y＜1 |
| D、0＜y＜x＜1 |