题目内容
对任意两实数a,b,定义运算“*”:a*b=
,关于函数f(-x)=e-x*ex,给出下列四个结论:
①函数f(x)的最小值是e;
②函数f(x)为偶函数;
③函数f(x)在(0,+∞)上单调递增;
④函数f(x)的图象与直线y=ex没有公共点;
其中正确结论的序号是( )
|
①函数f(x)的最小值是e;
②函数f(x)为偶函数;
③函数f(x)在(0,+∞)上单调递增;
④函数f(x)的图象与直线y=ex没有公共点;
其中正确结论的序号是( )
| A、①③ | B、②③ | C、①④ | D、②④ |
考点:函数解析式的求解及常用方法,函数的图象
专题:函数的性质及应用
分析:求出函数f(x)的解析式,求出函数的最小值判断①的正误;利用奇偶性定义判断②的正误;利用函数的单调性判断③的正误;利用函数的图象的交点判断④的正误.
解答:
解:由题意得,函数f(-x)=e-x*ex=
∴f(x)=
对于①,∵f(0)=e0=1,∴f(x)的最小值是1,∴①错误;
对于②,∵f(-x)=e-x*ex=ex*e-x=f(x),∴f(x)为偶函数,∴②正确;
对于③,当x>0时,f(x)=ex是增函数,∴③正确;
对于④,构造函数g(x)=ex-ex,其中x>0,当x=1时,g(x)=0,∴函数g(x)有零点,
∴函数f(x)与y=ex有公共点,∴④错误.
所以,正确的结论有②③.
故选:B.
|
∴f(x)=
|
对于①,∵f(0)=e0=1,∴f(x)的最小值是1,∴①错误;
对于②,∵f(-x)=e-x*ex=ex*e-x=f(x),∴f(x)为偶函数,∴②正确;
对于③,当x>0时,f(x)=ex是增函数,∴③正确;
对于④,构造函数g(x)=ex-ex,其中x>0,当x=1时,g(x)=0,∴函数g(x)有零点,
∴函数f(x)与y=ex有公共点,∴④错误.
所以,正确的结论有②③.
故选:B.
点评:本题考查了新定义的函数的性质以及应用问题,解题时应综合分析题目中的条件和结论,寻找解答问题的途径,是中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知a,b∈[-1,1],则函数f(x)=ax+b在区间(1,2)上存在一个零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在约束条件
下,目标函数z=x+2y的最大值为( )
|
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
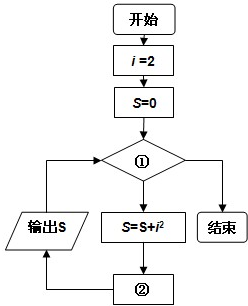 如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )
如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )| A、i≤2014,i=i+1 |
| B、i≤1007,i=i+1 |
| C、i≤2014,i=i+2 |
| D、i≤1007,i=i+2 |
已知命题p:“?x∈R,x2+1>0”命题q:“?x∈R,tanx=2”,则下列判断正确的是( )
| A、p∨q为真,¬p为真 |
| B、p∨q为假,¬p为假 |
| C、p∧q为真,¬p为真 |
| D、p∧q为真,¬p为假 |
设变量x,y满足不等式组
,则2x+3y的最大值等于( )
|
| A、1 | B、10 | C、41 | D、50 |
 如图,在△ABC中,AB=BC,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,BD=4,CD=2
如图,在△ABC中,AB=BC,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,BD=4,CD=2