Question

如图1，△ABC为正三角形，△BCD为等腰直角三角形，∠BCD=90°，将△ABC沿BC边折叠到△A′BC的位置，使A′B=A′D，E为BD中点，如图2．
（Ⅰ）求证：A′E⊥平面BCD；
（Ⅱ）求二面角B-A′C-D的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：空间角

分析：（Ⅰ）连结EC，由已知条件推导出A′E⊥BD，A′E⊥EC，由此能够证明A′E⊥平面BCD．
（Ⅱ）设BC=2，以ED、EC、EA为x，y，z轴，建立空间直角坐标系，利用向量法能二面角B-A′C-D的余弦值．

解答： （Ⅰ）证明：连结EC，∵E是BD的中点，∴A′E⊥BD，
又∵△BCD为等腰直角三角形，△ABC为正三角形，
∴A′E²=AB²-EC²，EC=BE，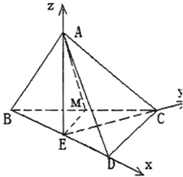
∴A′E²=A′B²-EC²=A′C²-EC²，
∴A′E⊥EC，
∴A′E⊥平面BCD．
（Ⅱ）设BC=2，以ED、EC、EA为x，y，z轴，
建立如图所示的空间直角坐标系，
则B（-

2

，0，0），D（

2

，0，0），C（0，

2

，0），A（0，0，

2

），
∴

CD

=(

2

，-

2

，0)，

CA

=(0，-

2

，

2

)，

BC

=(

2

，

2

，0)，
设平面A′DC的法向量

n1

=（x，y，z），
则

2 x- 2 y=0 - 2 y+ 2 z=0

，
取x=-2，得

n1

=（-2，-2，-2），
平面A′BC的法向量

n2

=（-2，2，2），
cos＜

n1

，

n2

＞=

4-4-4

12 • 12

=-

1

3

，
∴二面角B-A′C-D的余弦值为-

1

3

．

点评：本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．