题目内容

盒中装有5个乒乓球用作比赛，其中2个是旧球，另外3个是新球，新球使用后即成为了旧球．
（Ⅰ）每次比赛从盒中随机抽取1个球使用，使用后放回盒中，求第2次比赛结束后盒内剩余的新球数为2个的概率P；
（Ⅱ）每次比赛从盒中随机抽取2个球使用，使用后放回盒中，设第2次比赛结束后盒内剩余的新球数为X，求X的分布列和数学期望．
考点：离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题：概率与统计
分析：（Ⅰ）利用相互独立事件的概率乘法公式能求出第三产业次比赛结束后盒内剩余的新球数为2个的概率．
（Ⅱ）随机变量X的所有可能取值为0，1，2，3，分别求出P（X=3），P（X=2），P（X=1），P（X=0），由此能求出随机变量X有分布列和EX．
解答： 解：（Ⅰ）P=
2
5
×
2
5
+
3
5
×
3
5
=
13
25
．
（Ⅱ）随机变量X的所有可能取值为0，1，2，3，
P（X=3）=
C
2
2
C
2
2
C
2
5
C
2
5
=
1
100
，
P（X=2）=
C
2
2
C
1
3
C
1
2
+
C
1
3
C
1
2
C
2
3
C
2
5
C
2
5
=
24
100
，
P（X=1）=
C
2
2
C
2
3
+C
2
3
C
2
4
+C
1
3
C
1
2
C
1
3
C
1
2
C
2
5
C
2
5
=
57
100
，
P（X=0）=
C
2
3
C
1
4
C
1
1
+C
1
3
C
1
2
C
2
2
C
2
5
C
2
5
=
18
100
，
∴随机变量X有分布列为：
 X 0 1 23
P 
18
100
 
57
100
 
24
100
 
1
100
∴EX=0×
18
100
+1×
57
100
+2×
24
100
+3×
1
100
=
26
25
．
点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，在历年高考中都是必考题型之一．
练习册系列答案
相关题目
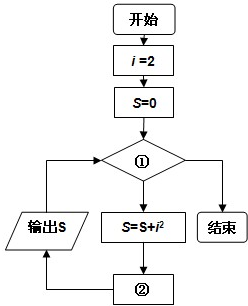如图是某青年歌手大奖赛上七位评委为某选手打出的分数的茎叶图（其中m为数字0-9中的一个）．若这组数据的中位数和平均数相等，则m=
 
．
如图分别表示输出22，22+42，22+42+62，…，22+42+62+…+20142值得过程的一个程序框图，那么在图中①②分别填上（　　）
A、i≤2014，i=i+1
B、i≤1007，i=i+1
C、i≤2014，i=i+2
D、i≤1007，i=i+2
设变量x，y满足不等式组
0≤x+y≤20
1≤y≤10
，则2x+3y的最大值等于（　　）
A、1B、10C、41D、50
已知a＞0，f（x）=
1
3
a2x3-ax2+
2
3
，g（x）=-ax+1，x∈R．
（1）当 a=1时，求 f（x）在点（1，f（1））处的切线方程；
（2）若在区间（0，
1
2
]上至少有一个实数x0，使 f（x0）＞g（x0），求a的取值范围．
某射击测试规则为：每人最多射击3次，击中目标即终止射击，第i次射击击中目标得i（i=1，2，3）分，3次均击中目标得0分．已知某射手每次击中目标的概率为0.8，各次射击结果互不影响．
（Ⅰ）求该射手至少射击两次并且击中目标的概率；
（Ⅱ）记该射手的得分为ξ，求随机变量ξ的分布列及数学期望．
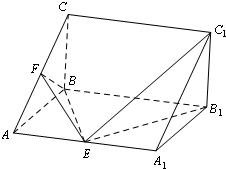如图，在三菱柱ABC-A1B1C1中，AA1B1B为矩形，平面AA1B1B⊥平面ABC．∠ABC=90°，AB=BC=
1
2
AA1=1，点F为AC的中点，点E为AA1上一点．
（1）求证：平面BEF⊥平面AA1C1C；
（2）当AE的长为何值时，二面角A1-C1E-B1为60°？
椭圆
x2
4
+y2=1的弦AB的中点为P(1，
1
2
)，则弦AB所在直线的方程是
 
．
设集合U={1，2，3，4}，A={1，2，4}，B={2，3，4}，则∁U（A∩B）等于（　　）
A、{1，2}
B、{1，4}
C、{1，3}
D、{2，4}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网