题目内容
在平面直角坐标系xOy中,已知曲线C1:
(θ为参数),将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的
、2倍后得到曲线C2的直角坐标方程为 .
|
| 3 |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把曲线C1的参数方程化为普通方程,根据坐标变换,得到曲线C2的直角坐标方程.
解答:
解:曲线C1的方程
(θ为参数)化为普通方程是x2+y2=1,
将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的
、2倍后,
得到曲线C2的直角坐标方程为
+
=1;
故答案为:
+
=1.
|
将曲线C1上的所有点的横坐标、纵坐标分别伸长为原来的
| 3 |
得到曲线C2的直角坐标方程为
| x2 |
| 3 |
| y2 |
| 4 |
故答案为:
| x2 |
| 3 |
| y2 |
| 4 |
点评:本题考查了曲线的参数方程化为普通方程以及普通方程的坐标变换问题,解题时应先把参数方程化为普通方程,再进行坐标变换,是基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
如果x>y>0,则
=( )
| xyyx |
| xxyy |
A、(x-y)
| ||
B、(x-y)
| ||
C、(
| ||
D、(
|
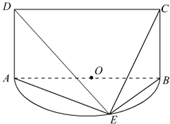 如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.
如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2a.
