题目内容
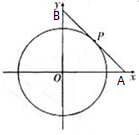 圆x2+y2=9的切线与x轴正半轴,y轴正半轴围成一个△AOB,切点为P,
圆x2+y2=9的切线与x轴正半轴,y轴正半轴围成一个△AOB,切点为P,(1)当|AB|最小时,求切线AB方程;
(2)若在x轴上存在异于点A的点M,在y轴上存在异于点B的点N,对圆x2+y2=9上任一点Q,有
| |AQ| |
| |MQ| |
| |BQ| |
| |NQ| |
考点:直线和圆的方程的应用
专题:计算题,证明题,直线与圆
分析:(1)用截距式设出切线方程,由圆心到直线的距离等于半径以及基本不等式可得ab=3
≤
,令t=
,可得t的最小值为6,此时a=b,即可得到切线方程;
(2)设出M,N,Q的坐标,运用两点的距离公式,列出等式,通过点Q的特殊点,求出M,N的坐标,再求斜率,计算直线OP与直线MN的斜率之和即可得证.
| a2+b2 |
| a2+b2 |
| 2 |
| a2+b2 |
(2)设出M,N,Q的坐标,运用两点的距离公式,列出等式,通过点Q的特殊点,求出M,N的坐标,再求斜率,计算直线OP与直线MN的斜率之和即可得证.
解答:
解:(1)设切线方程为
+
=1(a>0,b>0),即 bx+ay-ab=0,
∵圆心(0,0)到直线的距离等于半径得
=3,
∴ab=3
≤
,
令t=
,则有t2-6t≥0,t≥6,
则t的最小值为6,即|AB|的最小值为6,
此时a=b=3
,即有切线AB的方程为:x+y-3
=0;
(2)证明:设P(m,n),则过P的切线方程为mx+ny=9,
即有A(
,0),B(0,
),
设M(s,0),N(0,t),Q(x,y),
则
=
=c1,
由于对圆x2+y2=9上任一点Q,有
与
都是常数,
则可令Q(0,0),(3,0),则有
=
解得,s=
;
又
=
=c2,
可令Q(0,0),(0,3),则有
=
,解得,t=
,
直线OP的斜率为
,
直线MN的斜率为-
,
当m=n时,直线OP、MN的斜率互为相反数,
当m+n=6时,直线OP、MN的斜率互为相反数,但m2+n2=9,联立方程m+n=6,无解.
故在(1)的条件下,直线OP与直线MN的倾斜角互补.
| x |
| a |
| y |
| b |
∵圆心(0,0)到直线的距离等于半径得
| |0+0-ab| | ||
|
∴ab=3
| a2+b2 |
| a2+b2 |
| 2 |
令t=
| a2+b2 |
则t的最小值为6,即|AB|的最小值为6,
此时a=b=3
| 2 |
| 2 |
(2)证明:设P(m,n),则过P的切线方程为mx+ny=9,
即有A(
| 9 |
| m |
| 9 |
| n |
设M(s,0),N(0,t),Q(x,y),
则
| |AQ| |
| |MQ| |
| ||||
|
由于对圆x2+y2=9上任一点Q,有
| |AQ| |
| |MQ| |
| |BQ| |
| |NQ| |
则可令Q(0,0),(3,0),则有
| ||
| |s| |
3-
| ||
| |3-s| |
| 9 |
| 6-m |
又
| |BQ| |
| |NQ| |
| ||||
|
可令Q(0,0),(0,3),则有
| ||
| |t| |
3-
| ||
| (3-t| |
| 9 |
| 6-n |
直线OP的斜率为
| n |
| m |
直线MN的斜率为-
| 6-n |
| 6-m |
当m=n时,直线OP、MN的斜率互为相反数,
当m+n=6时,直线OP、MN的斜率互为相反数,但m2+n2=9,联立方程m+n=6,无解.
故在(1)的条件下,直线OP与直线MN的倾斜角互补.
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,基本不等式的运用,直线的截距式方程,利用了换元的思想,同时考查圆的又一定义,考查直线的斜率的运用,考查推理判断能力,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
直线的参数方程为
(t为参数),则直线的倾斜角为( )
|
| A、50° | B、40° |
| C、140° | D、130° |
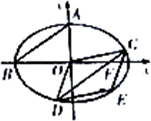 如图,椭圆
如图,椭圆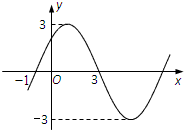 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,π)的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,π)的图象如图所示.