题目内容
函数y=sin（x+
）sin（
-x）的最小值是 ．
| π |
| 4 |
| π |
| 4 |
考点：三角函数的最值,二倍角的正弦
专题：三角函数的求值
分析：先根据两角和与差的正弦函数和二倍角公式对已知条件进行整理，再结合余弦函数的值域即可得到答案．
解答：
解：因为：y=sin（x+
）sin（
-x）=sin（x+
）cos（x+
）=
sin（2x+
）=
cos2x．
所以：cos2x=-1，函数有最小值：-
．
故答案为：-
．
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
所以：cos2x=-1，函数有最小值：-
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
点评：本题主要考查二倍角的余弦公式的逆用．解决这类问题的关键在于对公式的熟练掌握以及灵活运用．
练习册系列答案
相关题目
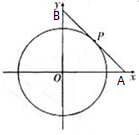圆x2+y2=9的切线与x轴正半轴，y轴正半轴围成一个△AOB，切点为P，