题目内容
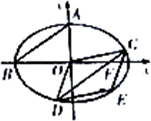 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意可知AB的斜率,进而根据点斜式表示出直线CD的方程,代入椭圆方程,进而可表示出CD的中点的坐标,则E点的坐标可得,代入椭圆方程即可证得结论.
解答:
证明:焦点为F(c,0),AB斜率为
,故CD的方程为y=
(x-c).
与椭圆联立后消去y,得2x2-2cx-b2=0,
∴xc+xd=c,
∴CD的中点为G(
,-
),
点E的坐标为(c,-
),
∵又离心率e=
,
∴E的坐标为(c,-
b)
∴将E代入椭圆方程得:
+
=e2+
=
+
=1成立,
故E在此椭圆上.
| b |
| a |
| b |
| a |
与椭圆联立后消去y,得2x2-2cx-b2=0,
∴xc+xd=c,
∴CD的中点为G(
| c |
| 2 |
| bc |
| 2a |
点E的坐标为(c,-
| bc |
| a |
∵又离心率e=
| ||
| 2 |
∴E的坐标为(c,-
| ||
| 2 |
∴将E代入椭圆方程得:
| c2 |
| a2 |
| ||
| b2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故E在此椭圆上.
点评:本题主要考查了椭圆的简单性质.考查了学生综合运用基础知识的能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若0≤θ<2π,
=(cos
,sin
),
=(cos
,-sin
),且满足
•
<0,那么θ的取值范围是( )
| a |
| θ |
| 2 |
| θ |
| 2 |
| b |
| θ |
| 2 |
| θ |
| 2 |
| a |
| b |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
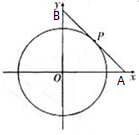 圆x2+y2=9的切线与x轴正半轴,y轴正半轴围成一个△AOB,切点为P,
圆x2+y2=9的切线与x轴正半轴,y轴正半轴围成一个△AOB,切点为P,