题目内容
3．在区间（0，3）上任取一个实数a，则不等式log2（4a-1）＜0成立的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{12}$ |
分析 根据对数的不等式的解法求出a的取值范围，结合几何概型的概率公式进行求解即可．
解答 解：由log2（4a-1）＜0得0＜4a-1＜1得$\frac{1}{4}$＜a＜$\frac{1}{2}$
在对应的概率P=$\frac{\frac{1}{2}-\frac{1}{4}}{3-0}=\frac{\frac{1}{4}}{3}$=$\frac{1}{12}$，
故选：D．
点评 本题主要考查几何概型的概率的计算，根据不等式的解法求出不等式的等价条件是解决本题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
14．
某校为了分析学生身体发育的状况，从一次体检中随机抽取了高三男生中20人的数据，将身高（单位：cm）用茎叶图记录如图；由此表估计该校高三男生身高在[165，175]的概率为（ ）
某校为了分析学生身体发育的状况，从一次体检中随机抽取了高三男生中20人的数据，将身高（单位：cm）用茎叶图记录如图；由此表估计该校高三男生身高在[165，175]的概率为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{9}{20}$ | C． | $\frac{11}{20}$ | D． | $\frac{1}{2}$ |
11．已知函数f（x）=2sin（ωx+$\frac{π}{6}$）（ω＞0）的图象与函数g（x）=cos（2x+φ）（|φ|＜$\frac{π}{2}$）的图象的对称中心完全相同，则φ=（ ）
| A． | $\frac{π}{6}$ | B． | -$\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | -$\frac{π}{3}$ |
8．已知复数z=$\frac{1}{i-1}$，则（ ）
| A． | z的实部为$\frac{1}{2}$ | B． | z的虚部为-$\frac{1}{2}$i | ||
| C． | |z|=$\frac{\sqrt{2}}{2}$ | D． | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
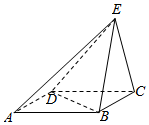如图，ABCD是平行四边形，已知$AB=2BC=4，BD=2\sqrt{3}$，BE=CE，平面BCE⊥平面ABCD．