题目内容
15.设p:实数x满足x2-(3a+1)x+2a2+a<0,q:实数x满足|x-3|<1.(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若a>0,且?p是?q的充分不必要条件,求实数a的取值范围.
分析 (1)由x2-(3a+1)x+2a2+a<0得(x-a)(x-(2a+1))<0,当a=1时,代入可得.由|x-3|<1,得-1<x-3<1,即可得出.利用p∧q为真,则p真且q真,即可得出.
(2)若¬p是¬q的充分不必要条件,可得q是p的充分不必要条件,即可得出.
解答 解:(1)由x2-(3a+1)x+2a2+a<0得(x-a)(x-(2a+1))<0,
当a=1时,1<x<3,即p为真时,实数x的取值范围是1<x<3.
由|x-3|<1,得-1<x-3<1,得2<x<4.
即q为真时实数x的取值范围是2<x<4,
若p∧q为真,则p真且q真,
∴实数x的取值范围是2<x<3.
(2)若¬p是¬q的充分不必要条件,
∴q是p的充分不必要条件,
则0<a≤2,且2a+1≥4
∴实数a的取值范围是$\frac{3}{2}$≤a≤2.
点评 本题考查了一元二次不等式的性质、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.设集合A={x|x≤1},B={x|x>a},且A∩B=∅,则实数a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
3.在区间(0,3)上任取一个实数a,则不等式log2(4a-1)<0成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
10.设Sn是公差d=-1的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则an=( )
| A. | -$\frac{1}{2}$-n | B. | $\frac{1}{2}$-n | C. | $\frac{1}{2}$+n | D. | -$\frac{1}{2}$+n |
20.已知集合A={x|log2x>0},B={x|x<1},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
7.已知$sinα=\frac{3}{5}$,且α为第二象限角,则$tan({2α+\frac{π}{4}})$=( )
| A. | $-\frac{19}{5}$ | B. | $-\frac{5}{19}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{17}{31}$ |
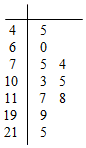 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.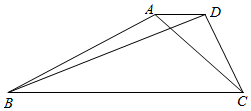 如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求:
如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求: