题目内容
18.将函数f(x)=Asin(ωx)(A≠0,ω>0)的图象向左平移$\frac{π}{6}$个单位,得到的图象关于原点对称,则ω的值可以为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据图象平移关系以及三角函数的对称性建立方程关系进行求解即可.
解答 解:f(x)=Asin(ωx)(A≠0,ω>0)的图象向左平移$\frac{π}{6}$个单位,得到y=Asinω(x+$\frac{π}{6}$)=Asin(ωx+$\frac{π}{6}$ω),
若图象关于原点对称,
则$\frac{π}{6}$ω=kπ,
即ω=6k,k∈Z
当k=1时,ω=6,
故选:D.
点评 本题主要考查三角函数的图象和性质,根据三角函数的图象平移关系求出函数的解析式,结合是就好像的对称性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知复数z=$\frac{2}{1+i}$+2i,则z的共轭复数是( )
| A. | -1-i | B. | 1-i | C. | 1+i | D. | -1+i |
3.在区间(0,3)上任取一个实数a,则不等式log2(4a-1)<0成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
10.设Sn是公差d=-1的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则an=( )
| A. | -$\frac{1}{2}$-n | B. | $\frac{1}{2}$-n | C. | $\frac{1}{2}$+n | D. | -$\frac{1}{2}$+n |
7.已知$sinα=\frac{3}{5}$,且α为第二象限角,则$tan({2α+\frac{π}{4}})$=( )
| A. | $-\frac{19}{5}$ | B. | $-\frac{5}{19}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{17}{31}$ |
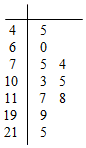 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.