题目内容
12.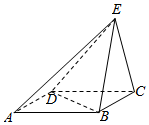 如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.(Ⅰ)证明:BD⊥CE;
(Ⅱ)若$BE=CE=\sqrt{10}$,求三棱锥B-ADE的高.
分析 (I)根据勾股定理的逆定理可证BD⊥BC,由面面垂直的性质可得BD⊥平面EBC,故BD⊥CE;
(II)取BC中点F,连接EF,DF,AF.则EF⊥平面ABCD,利用勾股定理求出EF,AF,DF,AE,DE,得出VE-ABD,S△ADE,根据等体积法计算棱锥的高.
解答  证明:(I)∵四边形ABCD是平行四边形,
证明:(I)∵四边形ABCD是平行四边形,
∴CD=AB=4,∵BC=2,BD=2$\sqrt{3}$,
∴BD2+BC2=CD2,∴BD⊥BC,
又平面BCE⊥平面ABCD,平面BCE∩平面ABCD=BC,BD?平面ABCD,
∴BD⊥平面BCE,∵CE?平面BCE,
∴BD⊥CE.
(II)取BC的中点F,连接EF,DF,AF.
∵EB=EC,
∴EF⊥BC,∵平面EBC⊥平面ABCD,平面EBC∩平面ABCD=BC,
∴EF⊥平面ABCD.
∵BE=CE=$\sqrt{10}$,BC=2,
∴EF=$\sqrt{B{E}^{2}-B{F}^{2}}=3$,DF=$\sqrt{B{D}^{2}+B{F}^{2}}$=$\sqrt{13}$,AF=$\sqrt{(AD+BF)^{2}+B{D}^{2}}$=$\sqrt{21}$,
∴DE=$\sqrt{E{F}^{2}+D{F}^{2}}$=$\sqrt{22}$,AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{30}$.
∴VE-ABD=$\frac{1}{3}{S}_{△ABD}•EF$=$\frac{1}{3}×\frac{1}{2}×2×2\sqrt{3}×3$=2$\sqrt{3}$.
cos∠AED=$\frac{22+30-4}{2×\sqrt{22}×\sqrt{30}}$=$\frac{12}{\sqrt{165}}$,∴sin∠AED=$\frac{\sqrt{21}}{\sqrt{165}}$.
∴S△ADE=$\frac{1}{2}AE•DEsin∠AED$=$\frac{1}{2}×\sqrt{30}×\sqrt{22}×\frac{\sqrt{21}}{\sqrt{165}}$=$\sqrt{21}$.
设B到平面ADE的高为h,
则VB-ADE=$\frac{1}{3}{S}_{△ADE}•h$=$\frac{\sqrt{21}}{3}h$=2$\sqrt{3}$,
∴h=$\frac{6\sqrt{7}}{7}$.
∴三棱锥B-ADE的高位$\frac{6\sqrt{7}}{7}$.
点评 本题考查了面面垂直的性质,棱锥的体积计算,属于中档题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
| A. | $-\frac{19}{5}$ | B. | $-\frac{5}{19}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{17}{31}$ |
| A. | 结构图 | B. | 散点图 | C. | 等高条形图 | D. | 残差图 |