题目内容
13.已知等比数列{an}的公比不为1,a1=$\frac{1}{2}$,且a1,2a2,4a3成等差数列.(1)求{an}的通项公式;
(2)求证:a1+a3+a5+…+a2n-1<$\frac{2}{3}$.
分析 (1)由a1,2a2,4a3成等差数列,可得2×2a2=a1+4a3,代入解出即可得出.
(2)由a2n-1=$(\frac{1}{2})^{2n-1}$,利用等比数列的前n项和公式即可得出.
解答 (1)解:∵a1,2a2,4a3成等差数列,∴2×2a2=a1+4a3,4×q=1+4q2,解得q=$\frac{1}{2}$.
∴an=$(\frac{1}{2})^{n}$.
(2)证明:a2n-1=$(\frac{1}{2})^{2n-1}$.
∴a1+a3+a5+…+a2n-1=$\frac{1}{2}$×$\frac{1-\frac{1}{{4}^{n}}}{1-\frac{1}{4}}$=$\frac{2}{3}$$(1-\frac{1}{{4}^{n}})$<$\frac{2}{3}$.
∴a1+a3+a5+…+a2n-1<$\frac{2}{3}$.
点评 本题考查了等差数列与等比数列的通项公式前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn,则S2015的值为( )
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4029}{4031}$ |
1.若$cosα=-\frac{5}{13}$,且α为第三象限角,则tanα的值等于( )
| A. | $\frac{12}{5}$ | B. | $-\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | $-\frac{5}{12}$ |
5.设集合A={x|x≤1},B={x|x>a},且A∩B=∅,则实数a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
2.设不等式组$\left\{\begin{array}{l}0≤x≤2\\ 0≤y≤2\end{array}\right.$表示的平面区域为D,在区域D内随机取一点M,则点M落在圆(x-1)2+y2=1内的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.在区间(0,3)上任取一个实数a,则不等式log2(4a-1)<0成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
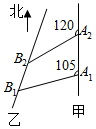 如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?
如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里? 如图,圆O与离心率为$\frac{\sqrt{3}}{2}$的椭圆T:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个切点为M(2,0),O为坐标原点.
如图,圆O与离心率为$\frac{\sqrt{3}}{2}$的椭圆T:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个切点为M(2,0),O为坐标原点.