题目内容

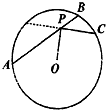如图，点P为圆O的弦AB上的任意点，连结PO，使∠OPC=90°，PC交圆于C，若AP=4，PC=3，则PB=
 
．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：确定P是圆O的PC所在弦的中点，利用相交弦定理PC2=AP•PB，即可得出结论．
解答： 解：∵点P为圆O的弦AB上的任意点，连结PO，使∠OPC=90°，
∴P是圆O的PC所在弦的中点，
∴PC2=AP•PB，
∵AP=4，PC=3，
∴9=4PB，
∴PB=
9
4
．
故答案为：
9
4
．
点评：本题考查垂径定理，考查相交弦定理，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
设椭圆
y2
a2
+
x2
b2
=1（a＞b＞0）两顶点A（-b，0），B（b，0），短轴长为4，焦距为2，过点P（4，0）的直线l与椭圆交于C，D两点．
（1）求椭圆的方程；
（2）求线段C，D中点Q的轨迹方程；
（3）若直线AC的斜率为1，在椭圆上求一点M，使三角形△MAC面积最大．
若椭圆E1：
x2
a12
+
y2
b12
=1和椭圆E2：
x2
a22
+
y2
b22
=1满足
a1
a2
=
b1
b2
=m（m＞0），则称这两个椭圆相似，m称为其相似比．
（1）求经过点（2，
6
），且与椭圆
x2
4
+
y2
2
=1相似的椭圆方程．
（2）设过原点的一条射线l分别与（1）中的两个椭圆交于A、B两点（其中点A在线段OB上），求|OA|+
1
|OB|
的最大值和最小值．
已知直线
3
x-y+2m=0与圆x2+y2=n2相切，其中n，m∈N*，n-m＜5，则满足条件的有序数对（m，n）的个数为
 
．
若不等式|x-a|-|x|＜2-a2对x∈R恒成立，则实数a的取值范围是
 
．
已知实数x、y满足：
y-x+2≥0
x2+y2≤4
，则z=y-
3
x的取值范围是
 
．
某高中共有学生1000名，其中高一年级共有学生380人．如果在全校学生中抽取1名学生，抽到高二年级学生的概率为0.37，现采用分层抽样（按年级分层）在全校抽取100人，则应在高三年级中抽取的人数等于
 
．
已知a，b，c分别为△ABC内角A，B，C的对边，在△ABC中，b=
2
a，且sinB+cosB=0，则角A的大小为
 
．
已知复数z=（2-i）i（其中i为虚数单位），则
.
z
=（　　）
A、2-iB、1+2i
C、-1+2iD、1-2i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网